Created by potrace 1.14, written by Peter Selinger 2001-2017
Seunghyun Oh
Machine Learning for Speech in Embedded System

CS224N W1. Basic concept and Framework in Nature Lanugage Process

 
  • Jul 13, 2021

All contents is arranged from CS224N contents. Please see the details to the CS224N!

1. One Hot Vector

  • Vector
\[\mathbb{R}^{|V| \times 1}\]
  • Example
\[w^{aardvar} = \begin{bmatrix} 1\\ 0\\ 0\\ \vdots\\ 0 \end{bmatrix}, w^{a} = \begin{bmatrix} 0\\ 1\\ 0\\ \vdots\\ 0 \end{bmatrix}, \dots w^{zebra}= \begin{bmatrix} 0\\ 0\\ 0\\ \vdots\\ 1 \end{bmatrix}\]

  • This word represents does not give us directly any notion of similarity.

    $(w^{hotel})^Tw^{motel} = (w^{motel})^Tw^{hotel} = 0$

2. SVD(Singular Value Decomposition) Base

$\checkmark$ What is the Singular Value Decomposition(SVD)?

  • For reducing the dimensionality
  • ${X = USV^T}$
  • Then, use the rows of U as the word embeddings for all words in our dictionary.
  • Word-Document Matrix
    • Loop over billions of documents and for each time word i appears in document j, we add one to entry $X_{ij}$
    • $\mathbb{R}^{ \lvert V \rvert\times M}$
    • M: the number of documents
  • Window-based Co-occurrence Matrix
    • Counting the number of times each word appears inside a window of a particular size around the word of interest.
    • Example( Window size = 1 )
      1. I enjoy flying.
      2. I like NLP.
      3. I like deep learning.

      The resulting counts matrix

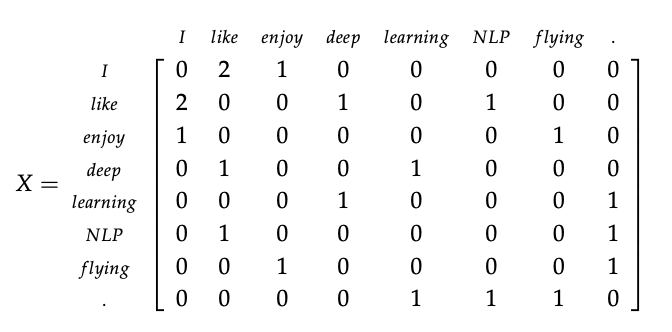
      Reference. cs224n-2019-notes01-wordvecs1

$\checkmark$ Applying SVD to the co-occurrence matrix

  • Cut SVD off at some index k based on the desired percentage variance captured(windows)

    $\dfrac { \textstyle\sum_{i=1}^k \sigma_i} { \textstyle\sum_{i=1}^{\lvert V \lvert}\sigma_i}$

  • Then take the sub-matrix of $U_{1:\lvert V \lvert,1:k}$ to be our word embedding matrix

  • Applying SVD to X:

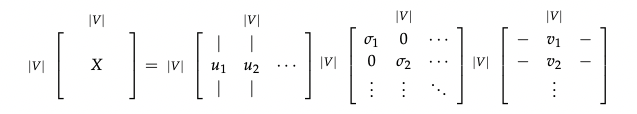
    Reference. cs224n-2019-notes01-wordvecs1

  • Reducing dimensionality by selecting first k singular vectors:

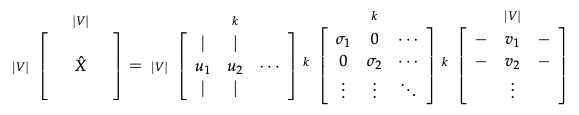
    Reference. cs224n-2019-notes01-wordvecs1

  • This method can encode semantic and syntactic (part of speech) information

$\checkmark$ Problem

  • The dimensions of the matrix change very often (new words are added very frequently and corpus changes in size).
  • The matrix is extremely sparse since most words do not co-occur.
  • The matrix is very high dimensional in general (≈ $10^6 \times 10^6$)
  • Quadratic cost to train (i.e. to perform SVD)
  • Requires the incorporation of some hacks on X to account for the drastic imbalance in word frequency

$\checkmark$ Some solution

  • Ignore function words such as “the”, “he”, “has”, etc.
  • Apply a ramp window – i.e. weight the co-occurrence count based on a distance between the words in the document.
  • Use Pearson correlation and set negative counts to 0 instead of using just raw count.

3. Iteration Based Methods

$\checkmark$ Word2vec

  • Probabilistic method

$\checkmark$ Language Models

  1. Unary Language model approach

    this probability by assuming the word occurrences are completely independent:

    $P(w_1,w_2,\dots, w_n) = \displaystyle\prod_{i=1}^{n}p(w_i)$

    • Issue
      • The next word is highly contingent upon the previous sequence of words.
      • The silly sentence example might actually score highly

  2. Bigram model

    $P(w_1,w_2,\dots, w_n) = \displaystyle\prod_{i=1}^{n}p(w_i\lvert w_{i-1})$

    • Issue: With pairs of neighboring words rather than evaluating a whole sentence.
    • In the Word-Word Matrix with a context of size 1, we basically can learn these pairwise probabilities.

$\checkmark$ Algorithm

$\checkmark$ Training methods

$\checkmark$ Evaluation and Training

4. Reference

Search