Quantization 1/2

이번 글에서는 MIT HAN LAB에서 강의하는 TinyML and Efficient Deep Learning Computing에 나오는 Quantization 방법을 두 차례에 걸쳐서 소개하려 한다. Quantization(양자화) 신호와 이미지에서 아날로그를 디지털로 변환하는 과정에서 사용하는 개념이다. 아래 그림과 같이 연속적인 센서로 부터 들어오는 아날로그 데이터 나 이미지를 표현하기 위해 단위 시간에 대해서 데이터를 샘플링하여 데이터를 수집한다.

Reference. MIT-TinyML-lecture5-Quantization-1 in https://efficientml.ai

디지털로 데이터를 변환하기 위해 데이터 타입을 정하면서 이를 하나씩 양자화한다. 양수와 음수를 표현하기 위해 Unsigned Integer 에서 Signed Integer, Signed에서도 Sign-Magnitude 방식과 Two’s Complement방식으로, 그리고 더 많은 소숫점 자리를 표현하기 위해 Fixed-point에서 Floating point로 데이터 타입에서 수의 범주를 확장시킨다. 참고로 Device의 Computationality와 ML 모델의 성능지표중 하나인 FLOP이 바로 floating point operations per second이다.

Reference. MIT-TinyML-lecture5-Quantization-1 in https://efficientml.ai

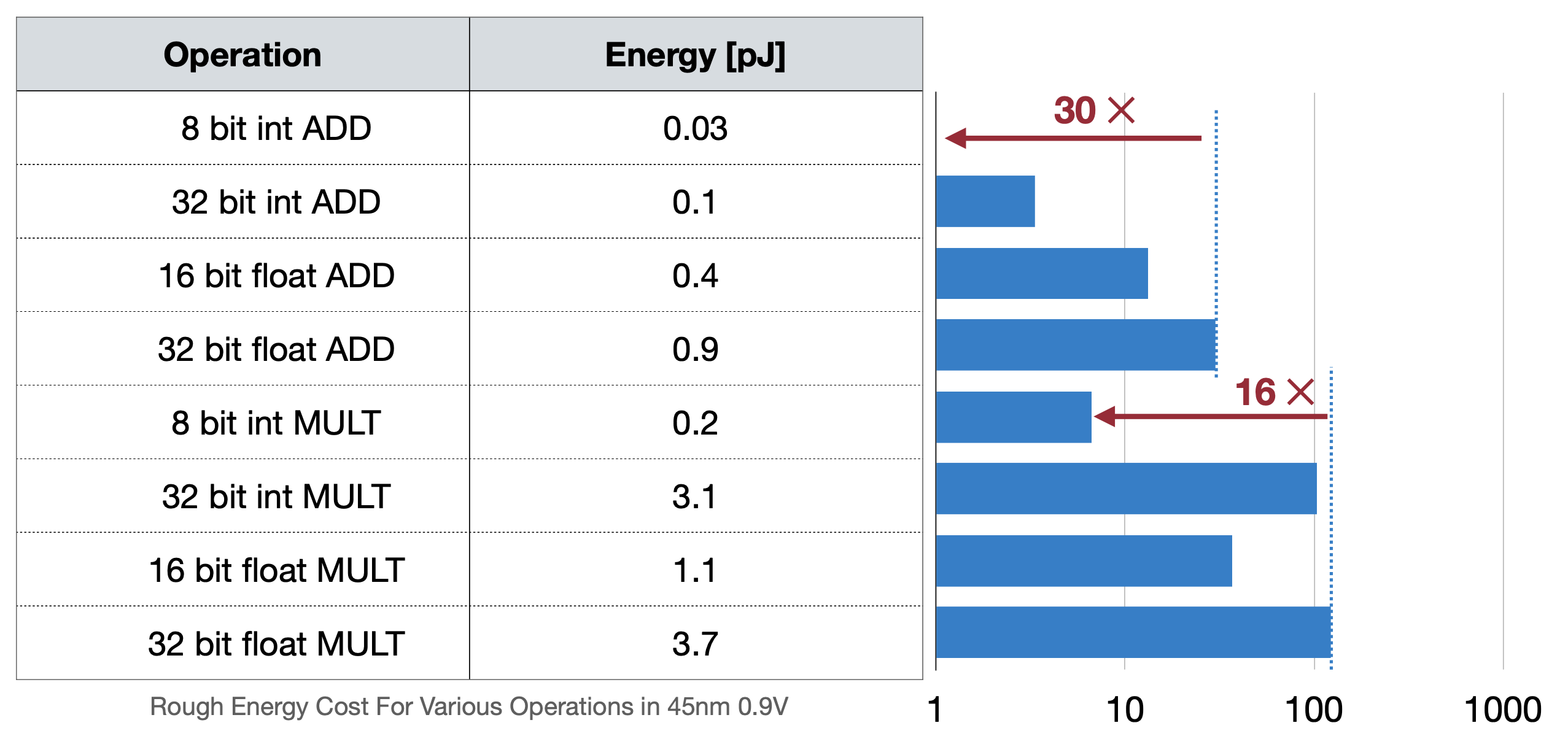
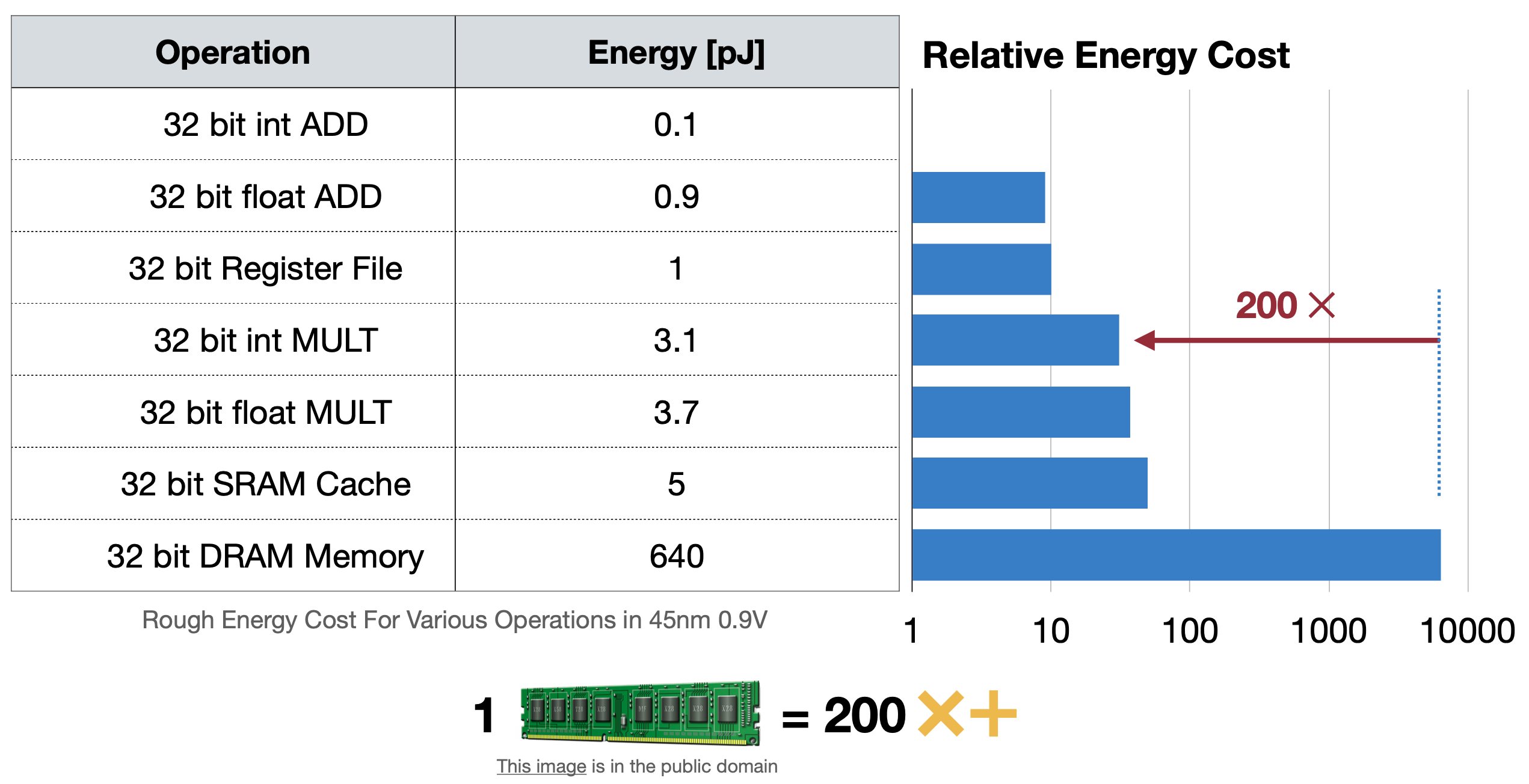
이 글에서 floating point를 이해하면, fixed point를 사용하는 것이 매모리에서, 그리고 연산에서 더 효율적일 것이라고 예상해볼 있 수 있다. ML모델을 클라우드 서버에서 돌릴 때는 크게 문제되지 않았지만 아래 두 가지 표를 보면 에너지소모, 즉 배터리 효율에서 크게 차이가 보인다. 그렇기 때문에 모델에서 Floating point를 fixed point로 더 많이 바꾸려고 하는데 이 방법으로 나온 것이 바로 Quatization이다.

이번 글에서는 Quntization 중에서 Quantization 방법과 그 중 Linear한 방법에 대해 더 자세하게, 그리고 Post-training Quantization까지 다루고, 다음 글에서는 Quantization-Aware Training, Binary/Tenary Quantization, Mixed Precision Quantization까지 다루려고 한다.

1. Common Network Quantization

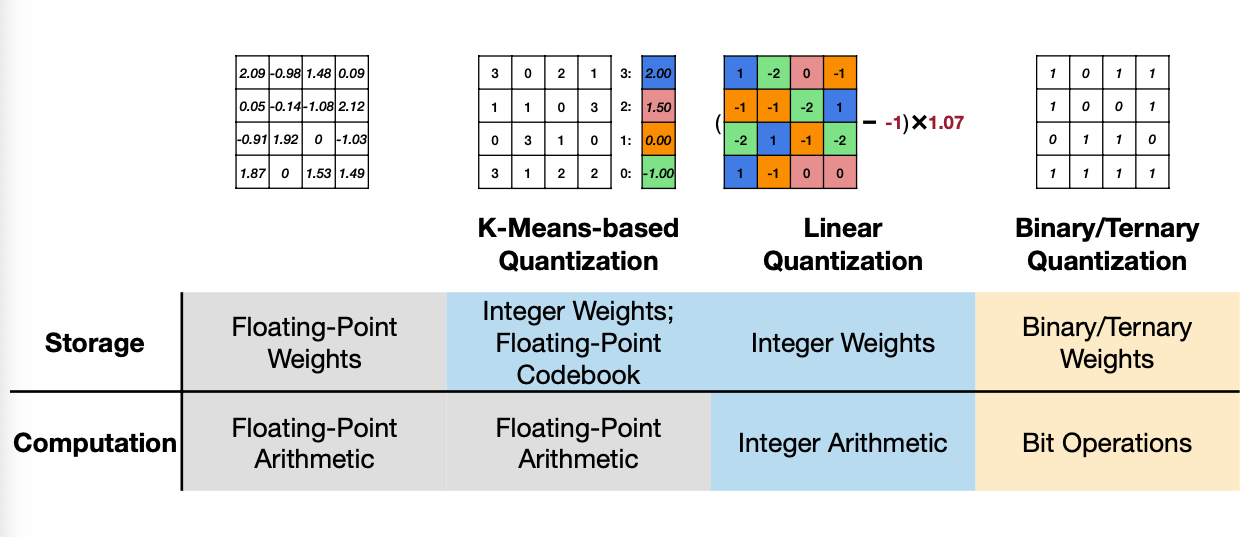
앞서서 소개한 것처럼 Neural Netowork를 위한 Quantization은 다음과 같이 나눌 수 있다. Quantization 방법을 하나씩 알아보자.

Reference. MIT-TinyML-lecture5-Quantization-1 in https://efficientml.ai

1.1 K-Means-based Quantization

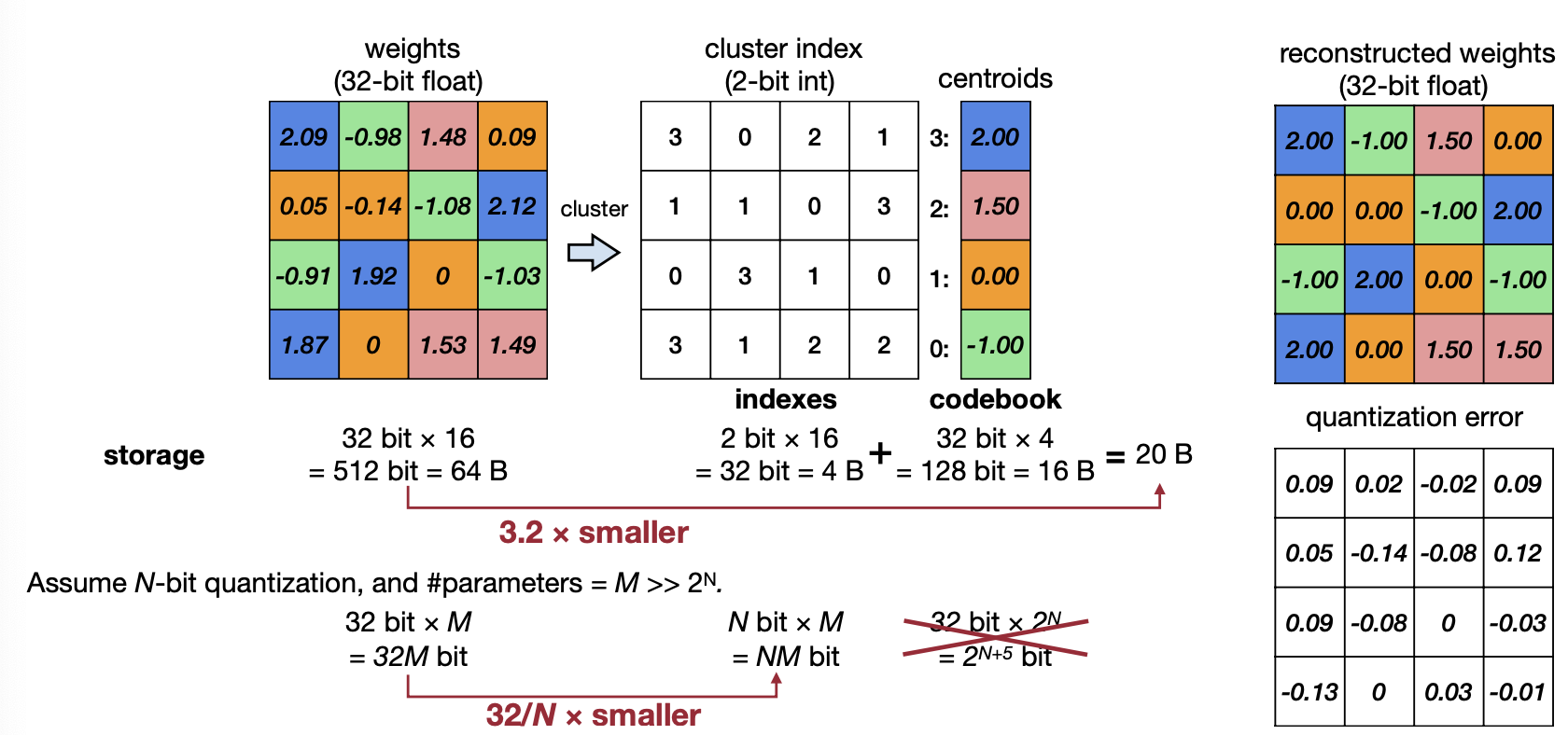
그 중 첫 번째로 K-means-based Quantization이 있다. Deep Compression [Han et al., ICLR 2016] 논문에 소개했다는 이 방법은 중심값을 기준으로 clustering을 하는 방법이다. 예제를 봐보자.

Reference. MIT-TinyML-lecture5-Quantization-1 in https://efficientml.ai

위 예제는 weight를 codebook에서 -1, 0, 1.5, 2로 나눠 각각에 맞는 인덱스로 표기한다. 이렇게 연산을 하면 기존에 64bytes를 사용했던 weight가 20bytes로 줄어든다. codebook으로 예제는 2bit로 나눴지만, 이를 N-bit만큼 줄인다면 우리는 총 32/N배의 메모리를 줄일 수 있다. 하지만 이 과정에서 quantizatio error, 즉 quantization을 하기 전과 한 후에 오차가 생기는 것을 위 예제에서 볼 수 있다. 메모리 사용량을 줄이는 것도 좋지만, 이 때문에 성능에 오차가 생기지 않게 하기위해 이 오차를 줄이는 것 또한 중요하다.

Reference. MIT-TinyML-lecture5-Quantization-1 in https://efficientml.ai

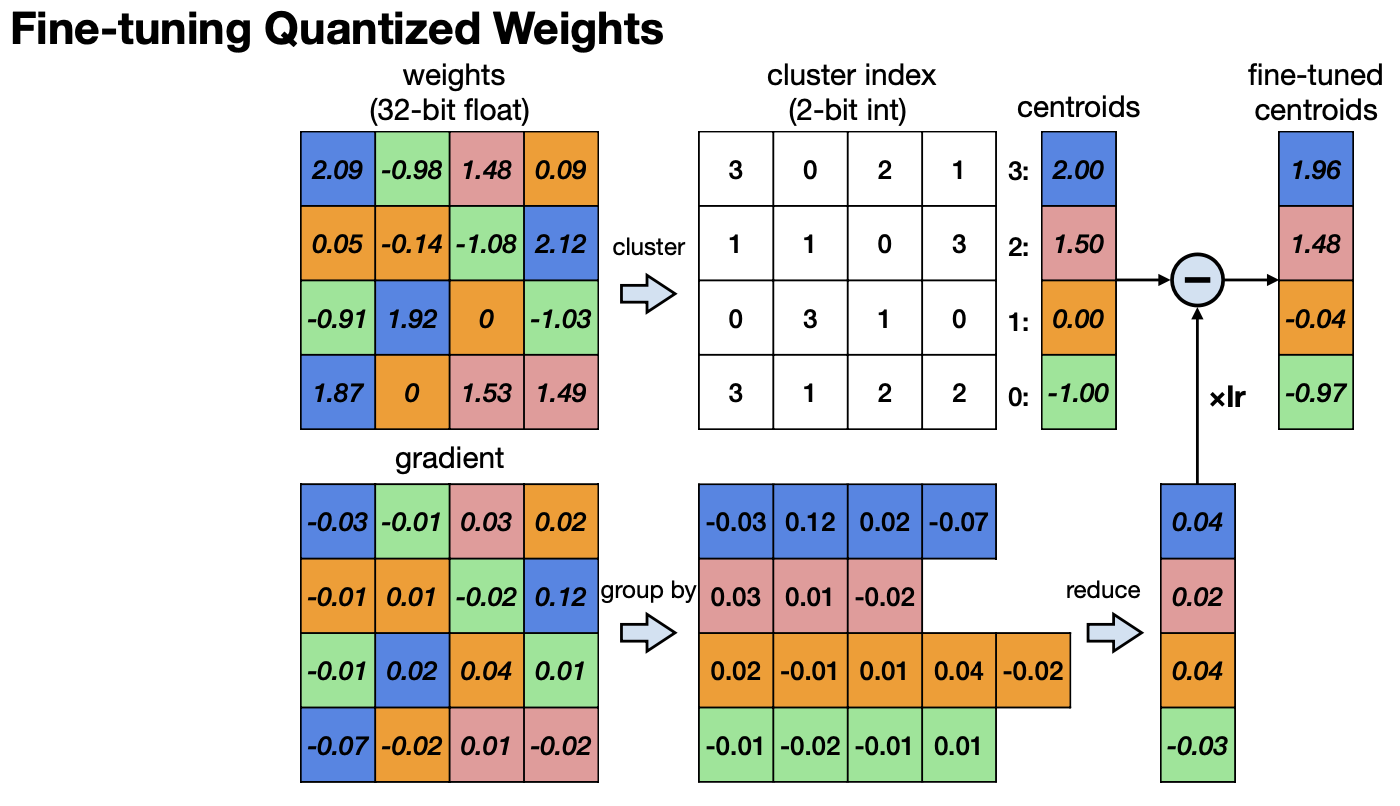
이를 보완하기 위해 Quantized한 Weight를 위에 그림처럼 Fine-tuning하기도 한다. centroid를 fine-tuning한다고 생각하면 되는데, 각 centroid에서 생기는 오차를 평균내 tuning하는 방법이다. 이 방법을 제안한 논문 에서는 Convolution 레이어에서는 4bit까지 centroid를 가졌을 때, Full-Connected layer에서는 2 bit까지 centroid를 가졌을 때 성능에 하락이 없다고 말하고 있었다.

Reference. Deep Compression [Han et al., ICLR 2016]

이렇게 Quantization 된 Weight는 위처럼 연속적인 값에서 아래처럼 Discrete한 값으로 바뀐다.

Reference. Deep Compression [Han et al., ICLR 2016]

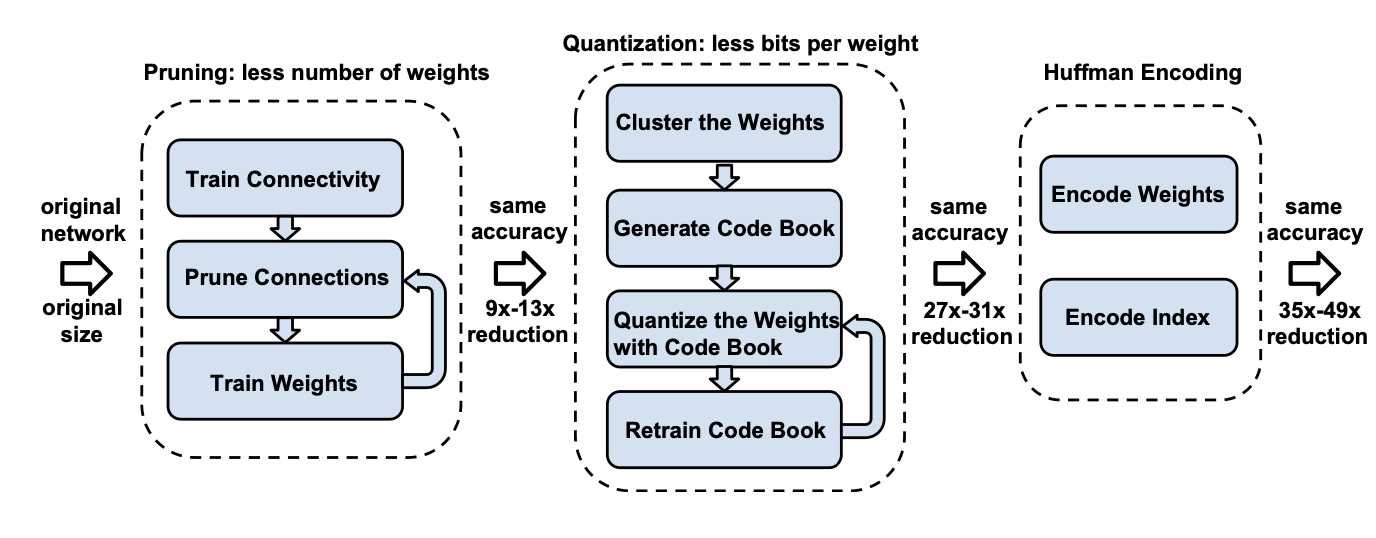
논문은 이렇게 Quantization한 weight를 한 번 더 Huffman coding를 이용해 최적화시킨다. 짧게 설명하자면, 빈도수가 높은 문자는 짧은 이진코드를, 빈도 수가 낮은 문자에는 긴 이진코드를 쓰는 방법이다. 압축 결과로 General한 모델과 압축 비율이 꽤 큰 SqueezeNet을 예로 든다. 자세한 내용은 논문을 참고하는 걸로.

Reference. Deep Compression [Han et al., ICLR 2016]

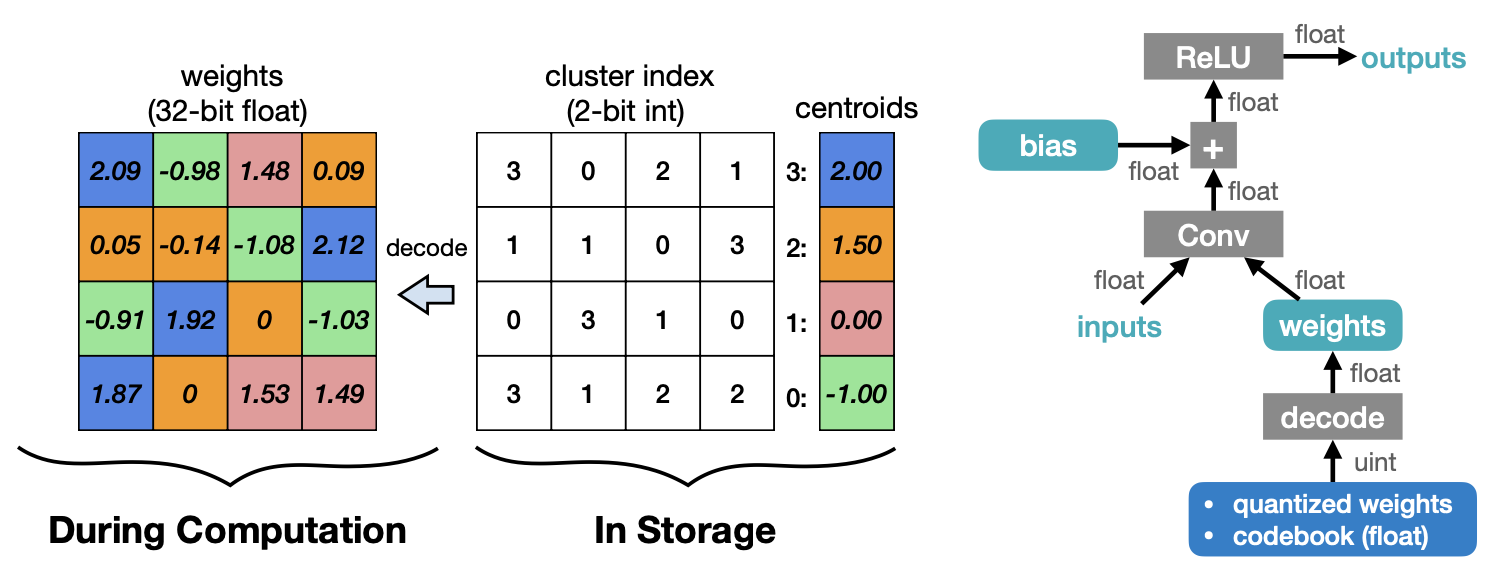
inference를 위해 weight를 Decoding하는 과정은 inference과정에서 저장한 cluster의 인덱스를 이용해 codebook에서 해당하는 값을 찾아내는 것이다. 이 방법은 저장 공간을 줄일 수는 있지만, floating point Computation이나 메모리 접근하는 방식으로 centroid를 쓰는 한계가 있을 수 밖에 없다.

Reference. Deep Compression [Han et al., ICLR 2016]

1.2 Linear Quantization

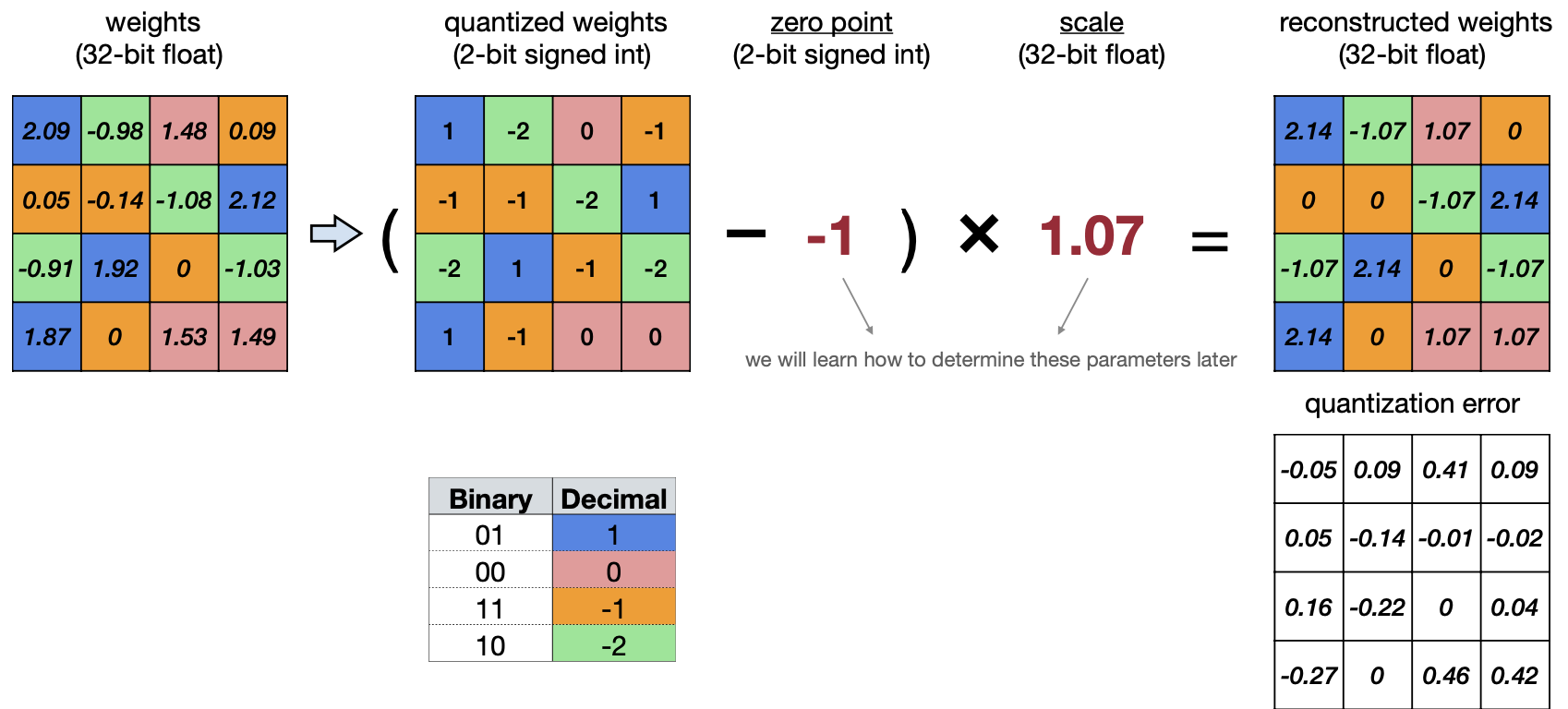
두 번째 방법은 Linear Quatization이다. floating-point인 weight를 N-bit의 정수로 affine mapping을 시키는 방법이다. 간단하게 식으로 보는 게 더 이해가 쉽다.

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

여기서 S(Scale of Linear Quantization)와 Z(Zero point of Linear Quantization)가 있는데 이 둘이 quantization parameter 로써 tuning을 할 수 있는 값인 것이다.

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

1.3 Scale and Zero point

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

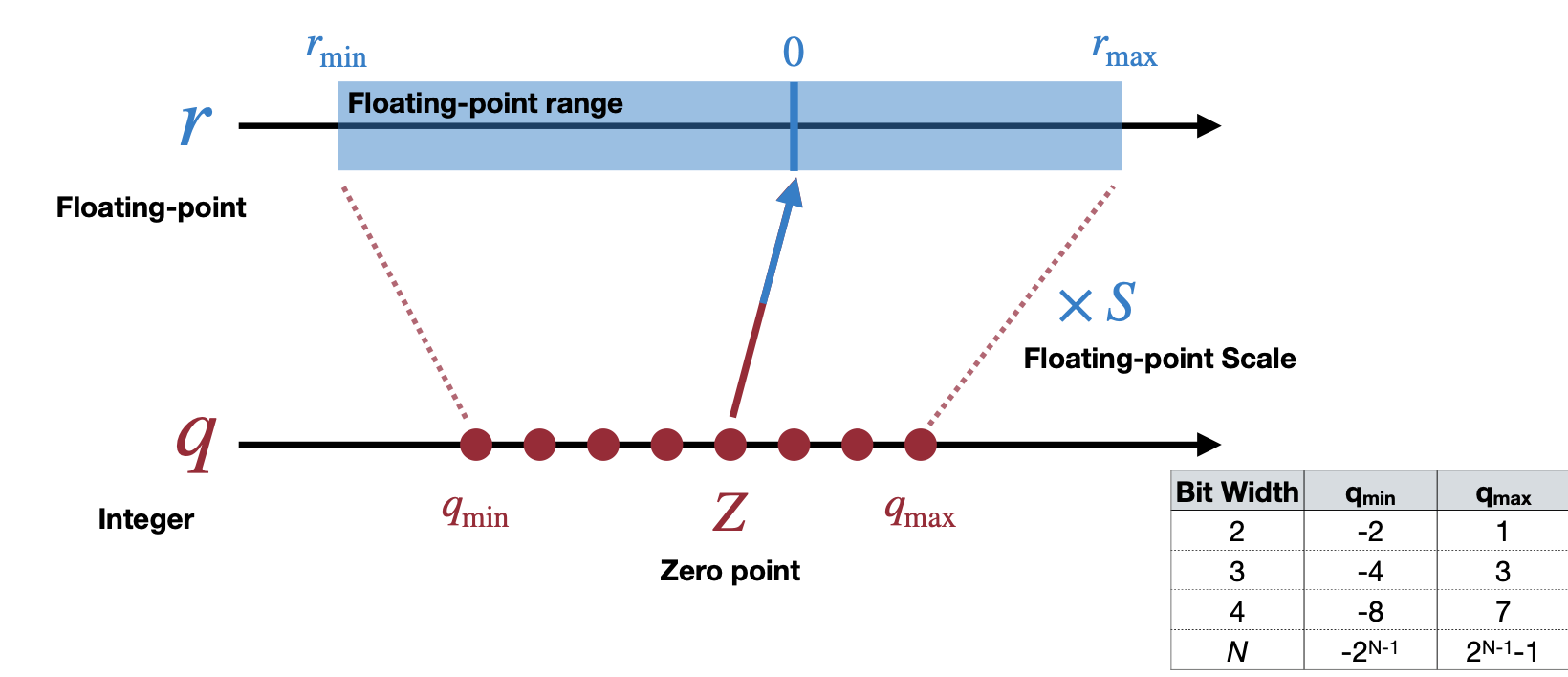
이 Scale과 Zero point 두 파라미터를 이용해서 affine mapping은 위 그림과 같다. Bit 수(Bit Width)가 낮아지면 낮아질 수록, floating point에서 표현할 있는 수 또한 줄어들 것이다. 그렇다면 Scale와 Zero point는 각각 어떻게 계산할까?

우선 floating-point 인 숫자의 범위 중 최대값과 최솟값에 맞게 두 식을 세우고 이를 연립방정식으로 Scale과 Zero point을 구할 수 있다.

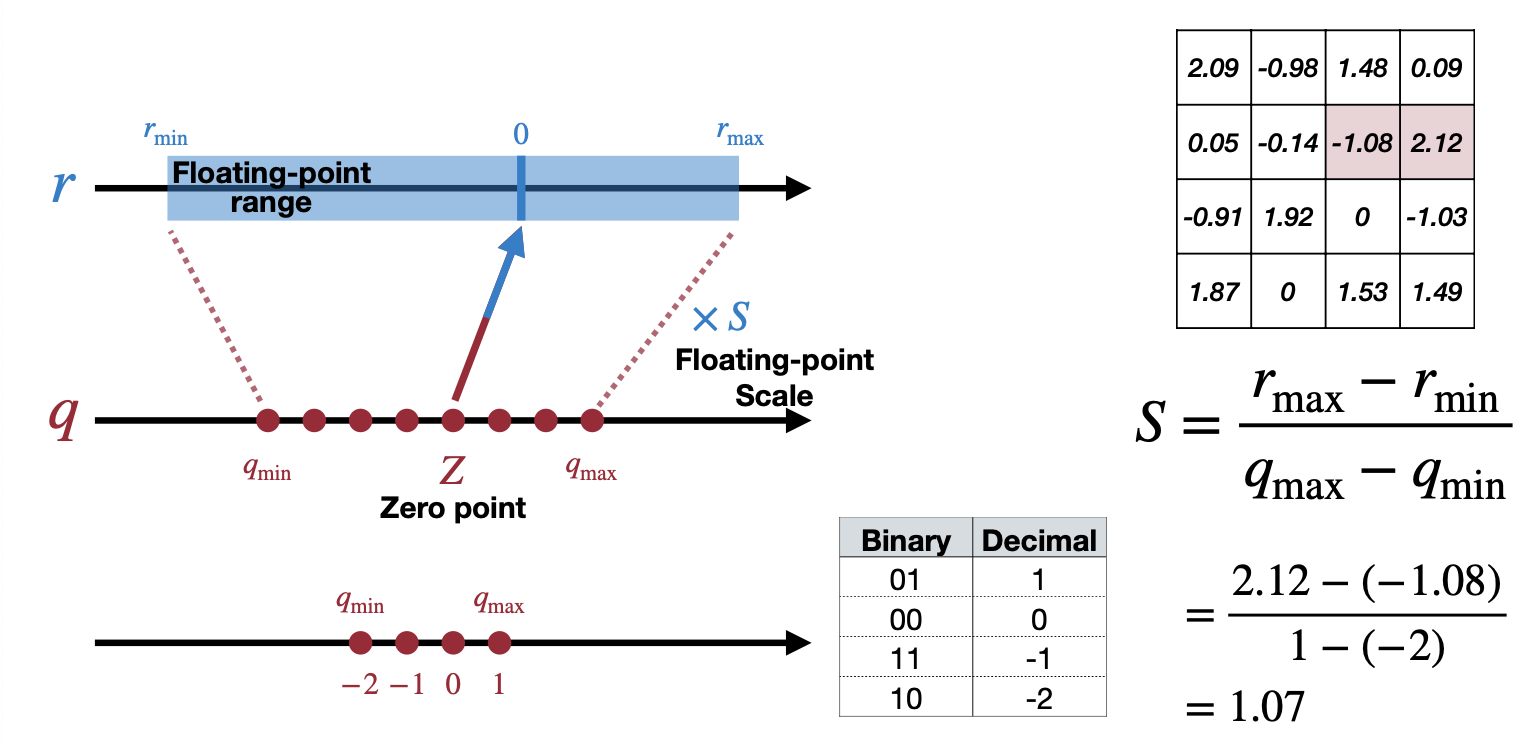
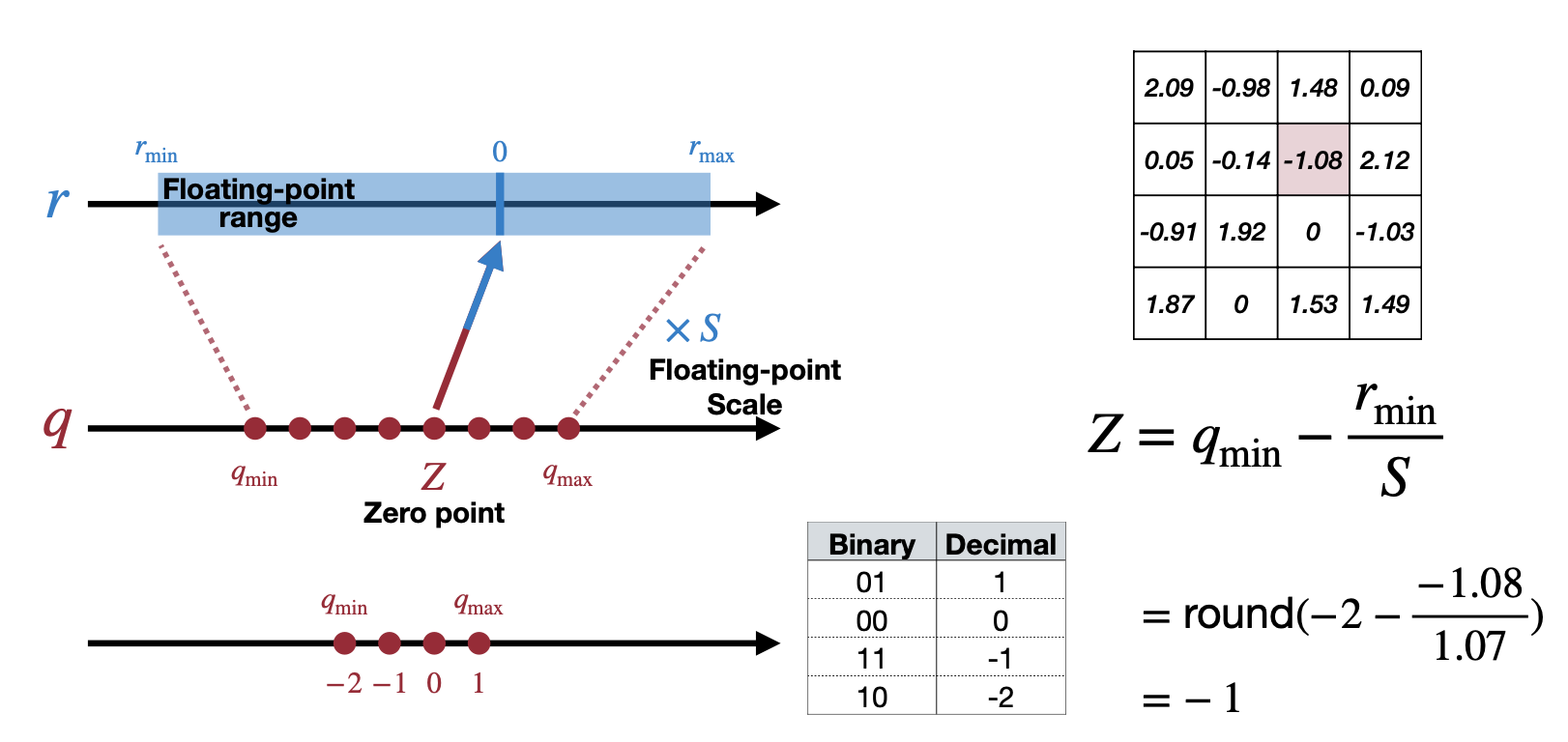
\[r_{max} = S(q_{max}-Z) \\ r_{min} = S(q_{min}-Z) \\ r_{max} - r_{min} = S(q_{max} - q_{min})\\ S = \dfrac{r_{max}-r_{min}}{q_{max}-q_{min}} \\ \\\] \[r_{min} = S(q_{min}-Z)\\ Z=q_{min}-\dfrac{r_{min}}{S}\\ Z = round\Big(q_{min}-\dfrac{r_{min}}{S}\Big)\]

예를 들어, 아래와 같은 예제에서 \(r_{max}\) 는\(2.12\) 이고 \(r_{min}\) 은 \(-1.08\) 로 Scale을 계산하면 아래 그림처럼 된다. Zero point는 \(-1\) 로 계산할 수 있다.

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

그럼 Symmetric하게 r의 범위를 제한하는 것과 같은 다른 Linear Quantization은 없을까? 이를 앞서, Quatized된 값들이 Matrix Multiplication을 하면서 미리 계산될 수 있는 수 (Quantized Weight, Scale, Zero point)가 있으니 inference시 연산량을 줄이기 위해 미리 계산할 수 있는 파라미터는 없을까?

1.4 Quantized Matrix Multiplication

입력 X, Weight W, 결과 Y가 Matrix Multiplication을 했다고 할 때 식을 계산해보자.

\[Y=WX \\ \\ S_Y(q_Y-Z_Y) = S_W(q_W-Z_W) \cdot S_X(q_X-Z_X)\\ \vdots \\\]

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

여기서 마지막 정리한 식을 살펴보면,

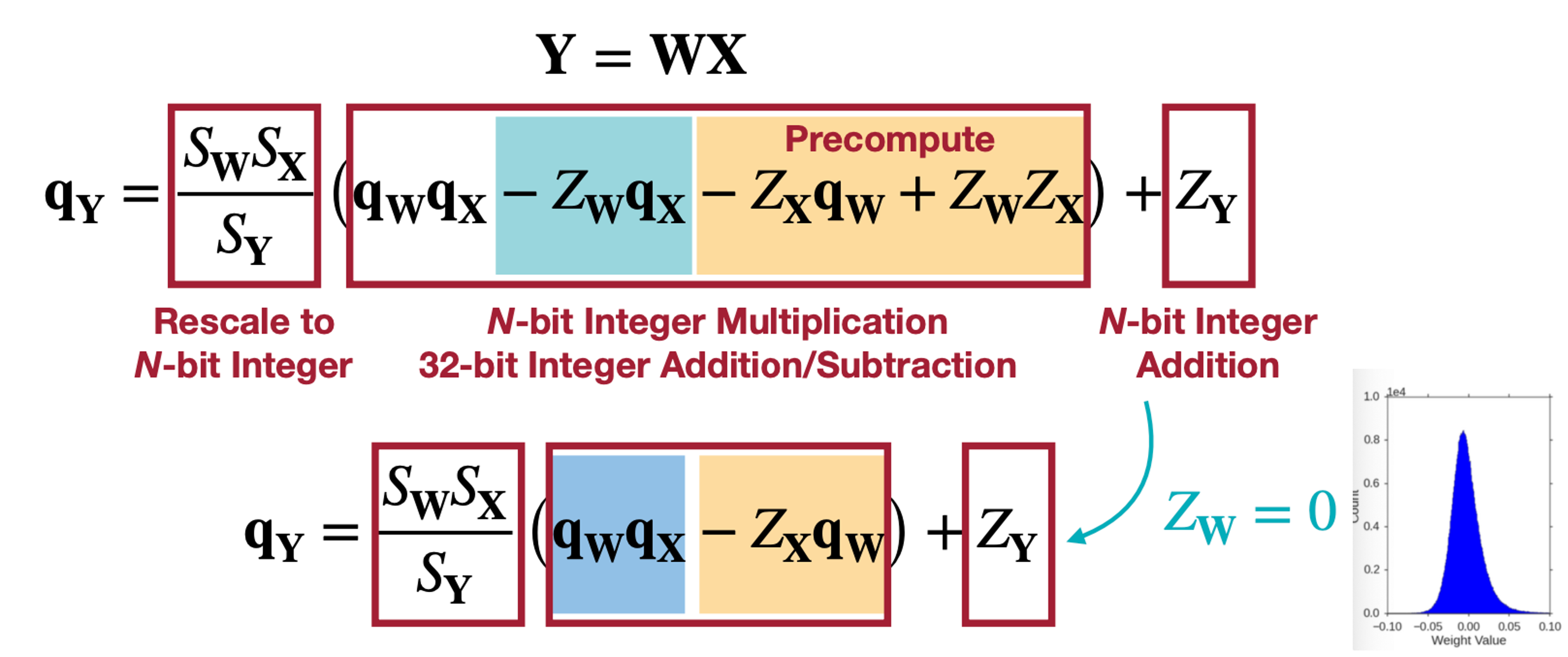
\(Z_x\) 와 \(q_w, Z_w, Z_X\) 의 경우는 미리 연산이 가능하다. 또 \(S_wS_X/S_Y\) 의 경우 항상 수의 범위가 \((0, 1)\) 로 \(2^{-n}M_0\) , \(M_0 \in [0.5, 1)\) 로 변형하면 N-bit Integer로 Fixed-point 형태로 표현 가능하다. 여기에 \(Z_w\)가 0이면 어떨까? 또 미리 계산할 수 있는 항이 보인다.

1.5 Symmetric Linear Quantization

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

\(Z_w = 0\) 이라고 함은 바로 위와 같은 Weight 분포인데, 바로 Symmetric한 Linear Quantization으로 \(Z_w\)를 0으로 만들어 \(Z_w q_x\)항을 0으로 둘 수 있어 연산을 또 줄일 수 있을 것이다.

Symmetric Linear Quantization은 주어진 데이터에서 Full range mode와 Restrict range mode로 나뉜다.

첫 번째 Full range mode 는 Scale을 real number(데이터, weight)에서 범위가 넓은 쪽에 맞추는 것이다. 예를 들어 아래의 경우, r_min이 r_max보다 절댓값이 더 크기 때문에 r_min에 맞춰 q_min을 가지고 Scale을 구한다. 이 방법은 Pytorch native quantization과 ONNX에서 사용된다고 강의에서 소개한다.

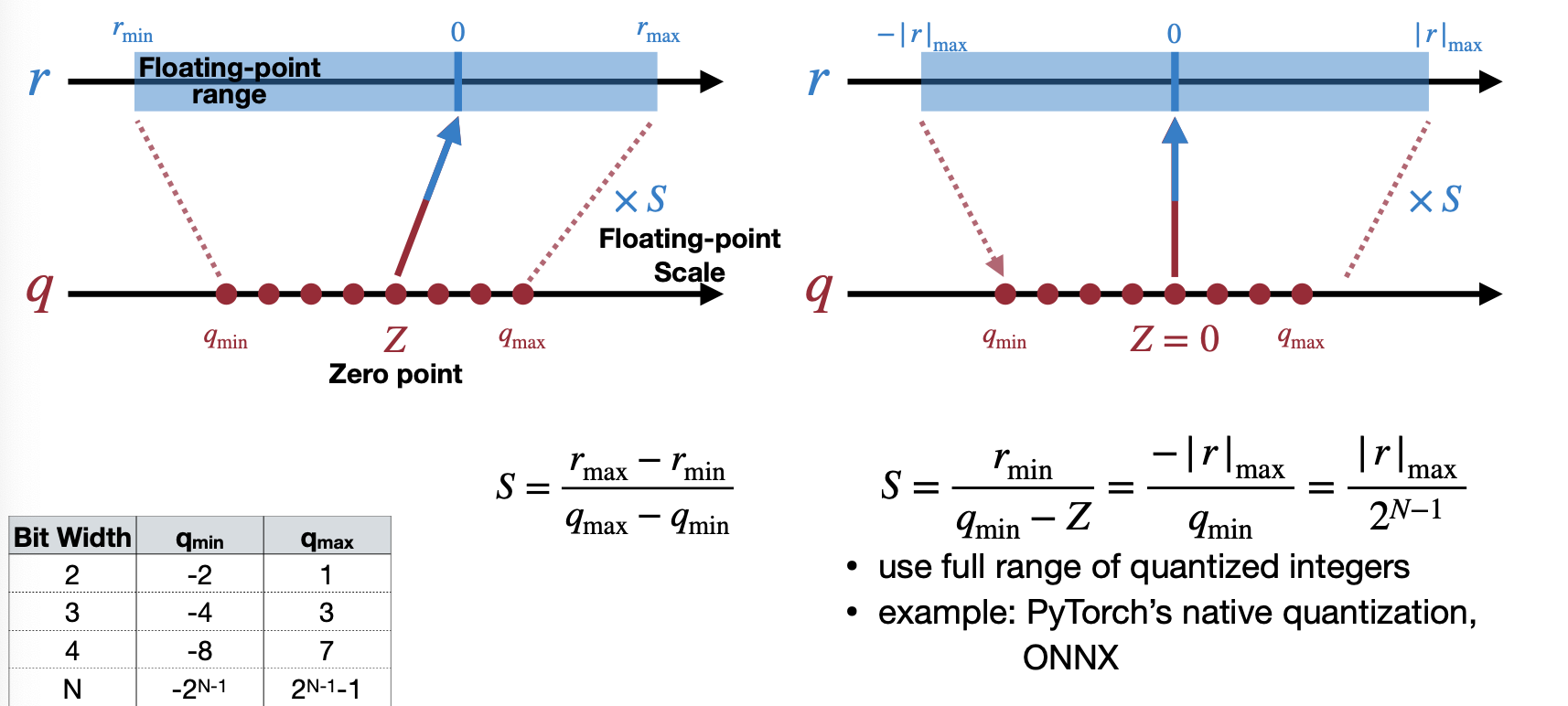
Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

두 번째 Restrict range mode는 Scale을 real number(데이터, weight)에서 범위가 좁은 쪽에 맞추는 것이다. 예를 들어 아래의 경우, r_min가 r_max보다 절댓값이 더 크기 때문에 r_min에 맞추면서 q_max에 맞도록 Scale을 구한다. 이 방법은 TensorFlow, NVIDIA TensorRT, Intel DNNL에서 사용된다고 강의에서 소개한다.

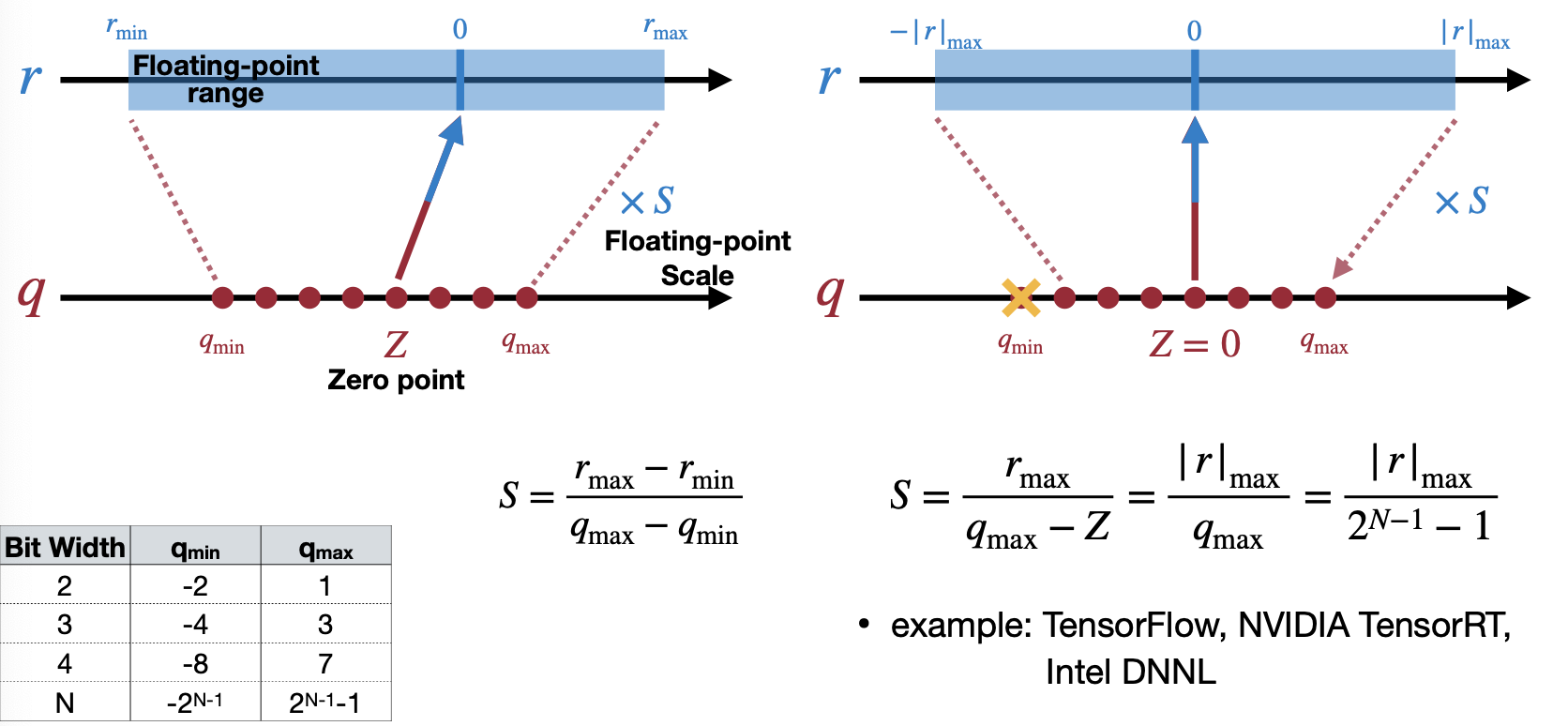
Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

그렇다면 왜 Symmetric 써야할까? Asymmetric 방법과 Symmetric 방법의 차이는 뭘까? (feat. Neural Network Distiller) 아래 그림을 참고하면 되지만, 가장 큰 차이로 보이는 것은 Computation vs Compactful quantized range로 이해간다.

Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

1.6 Linear Quantization examples

그럼 Quatization 방법에 대해 알아봤으니 이를 Full-Connected Layer, Convolution Layer에 적용해보고 어떤 효과가 있는지 알아보자.

1.6.1 Full-Connected Layer

아래처럼 식을 전개해보면 미리 연산할 계산할 수 있는 항과 N-bit integer로 표현할 있는 항으로 나눌 수 있다(전개하는 이유는 아마 미리 계산할 수 있는 항을 알아보기 위함이 아닐까 싶다).

\[\begin{aligned} Y=&WX+b \\ \downarrow& \\ S_Y(q_Y - Z_Y) = S_W(q_W - Z_W&) \cdot S_X(q_X - Z_X) + S_b(q_b - Z_b)\\ \downarrow& \ Z_w=0 \\ S_Y(q_Y - Z_Y) = S_WS_X(q_W&q_X - Z_xq_W) + S_b(q_b - Z_b)\\ \downarrow& \ Z_b=0, S_b=S_WS_X \\ S_Y(q_Y - Z_Y) = S_W&S_X(q_Wq_X - Z_xq_W+q_b)\\ \downarrow& \\ q_Y = \dfrac{S_WS_X}{S_Y}(q_Wq_X&+q_b - Z_Xq_W) + Z_Y\\ \downarrow& \ q_{bias}=q_b-Z_xq_W\\ q_Y = \dfrac{S_WS_X}{S_Y}(q_W&q_X+ q_{bias}) + Z_Y\\ \end{aligned}\]

간단히 표기하기 위해 \(Z_W=0, Z_b=0, S_b = S_W S_X\) 이라고 가정한다.

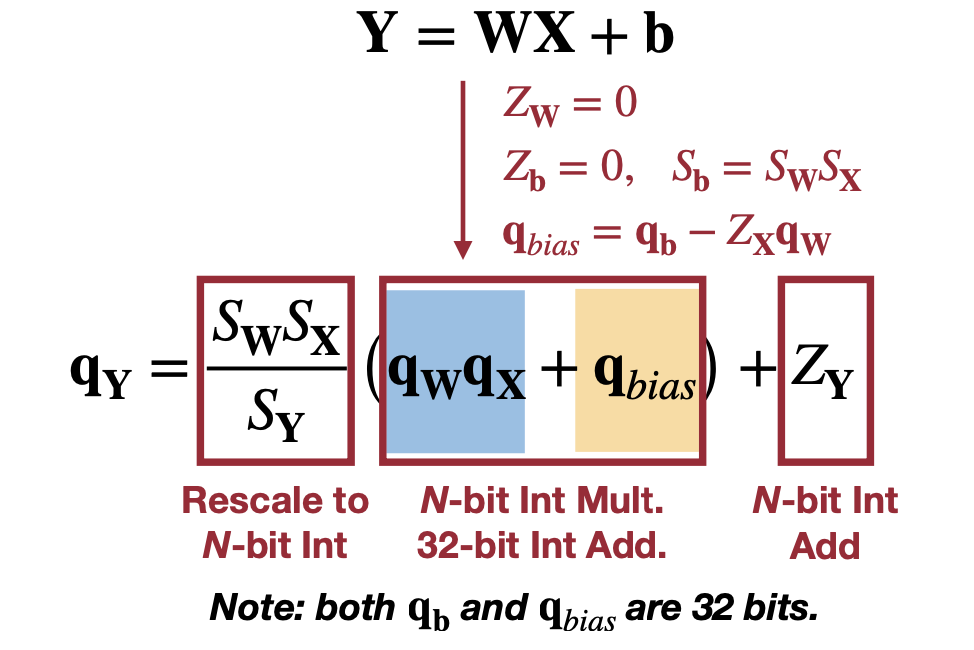
Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

1.6.2 Convolutional Layer

Convolution Layer의 경우는 Weight와 X의 곱의 경우를 Convolution으로 바꿔서 생각해보면 된다. 그도 그럴 것이 Convolution은 Kernel과 Input의 곱의 합으로 이루어져 있기 때문에 Full-Connected와 거의 유사하게 전개될 수 있을 것이다.

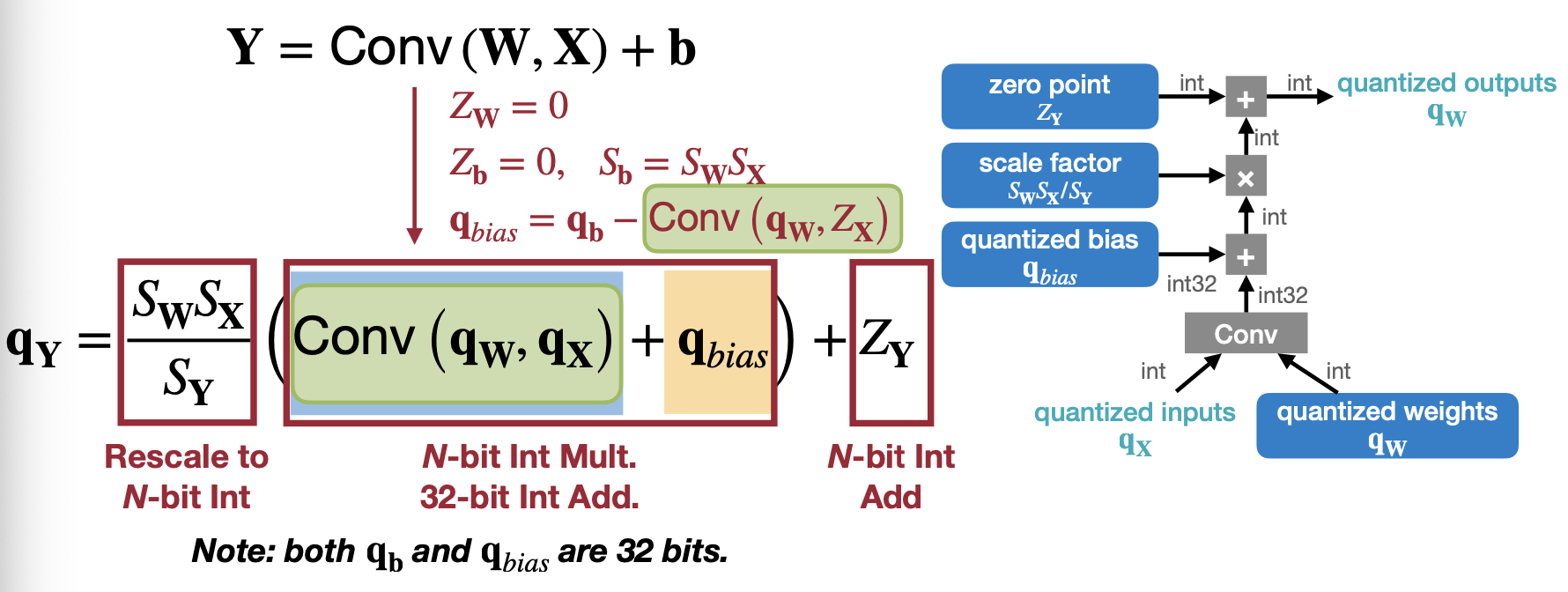
Reference. MIT-TinyML-lecture05-Quantization-1 in https://efficientml.ai

2. Post-training Quantization (PTQ)

그럼 앞서서 Quantizaed한 Layer를 Fine tuning할 없을까? “How should we get the optimal linear quantization parameters (S, Z)?” 이 질문에 대해서 Weight, Activation, Bias 세 가지와 그에 대하여 논문에서 보여주는 결과까지 알아보자.

2.1 Weight quantization

TL;DR. 이 강의에서 소개하는 Weight quantization은 Grandularity에 따라 Whole(Per-Tensor), Channel, 그리고 Layer로 들어간다.

2.1.1 Granularity

Weight quantization에서 Granularity에 따라서 Per-Tensor, Per-Channel, Group, 그리고 Generalized 하는 방법으로 확장시켜 Shared Micro-exponent(MX) data type을 차례로 보여준다. Scale을 몇 개나 둘 것이냐, 그 Scale을 적용하는 범위를 어떻게 둘 것이냐, 그리고 Scale을 얼마나 디테일하게(e.g. floating-point)할 것이냐에 초점을 둔다.

Reference. MIT-TinyML-lecture05-Quantization-2 in https://efficientml.ai

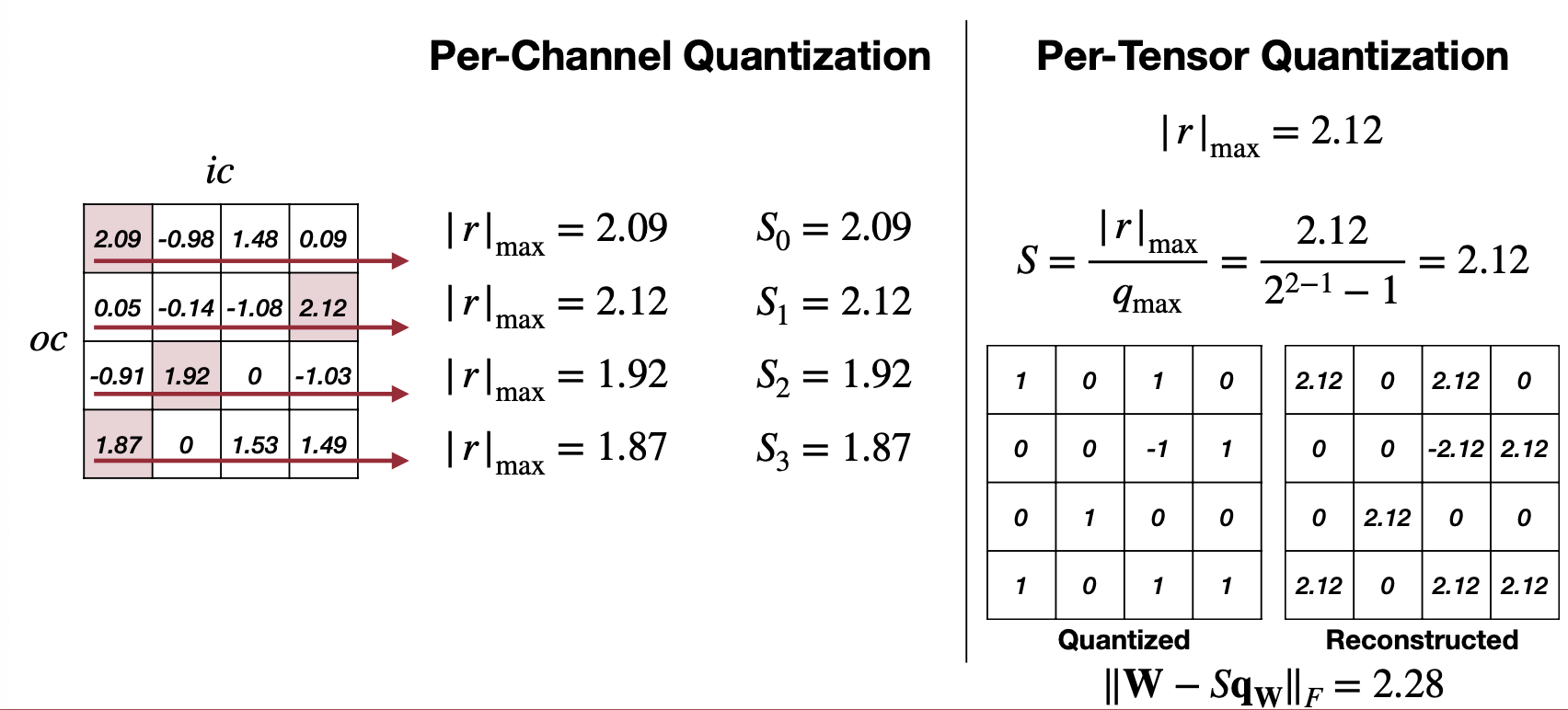
첫 번째는 Per-Tensor Quantization 특별하게 설명할 것 없이 이전까지 설명했던 하나의 Scale을 사용하는 Linear Quantization이라고 생각하면 되겠다. 특징으로는 Large model에 대해서는 성능이 괜찮지만 작은 모델로 떨어지면 성능이 급격하게 떨어진다고 설명한다. Channel별로 weight 범주가 넓은 경우나 outlier weight가 있는 경우 quantization 이후에 성능이 하락했다고 말한다.

Reference. MIT-TinyML-lecture05-Quantization-2 in https://efficientml.ai

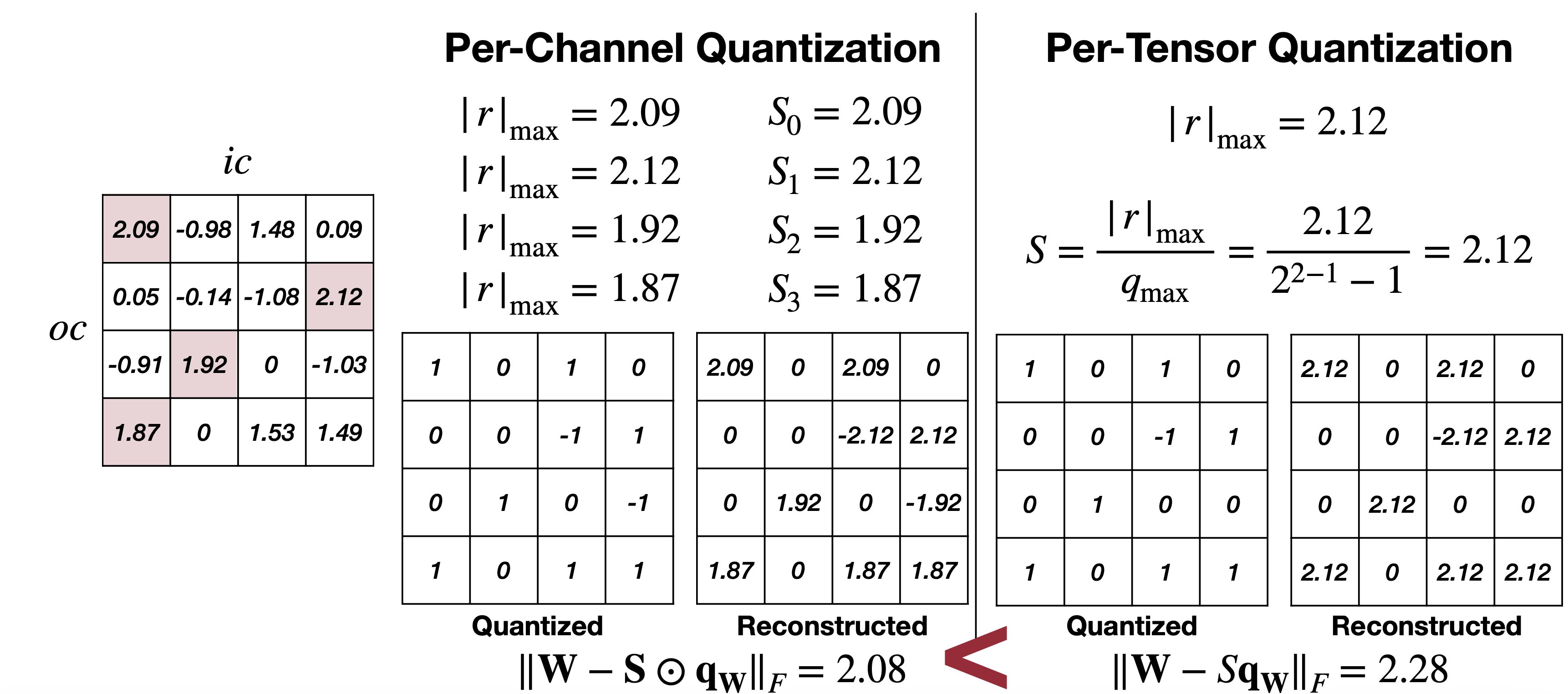
그래서 그 해결방안으로 나오는 것이 두 번째 방법인 Per-Channel Quantization이다. 위 예제에서 보면 Channel 마다 최대값과 각각에 맞는 Scale을 따로 가지는 것을 볼 수 있다. 그리고 적용한 결과인 아래 그림을 보면 Per-Channel과 Per-Tensor를 비교해보면 Per-Channel이 기존에 floating point weight와의 차이가 더 적다. 하지만, 만약 하드웨어에서 Per-Channel Quantization을 지원하지 않는다면 불필요한 연산을 추가로 해야하기 때문에 이는 적합한 방법이 될 수 없다는 점도 고려해야할 것이다(이는 이전 Tiny Engine에 대한 글에서 Channel내에 캐싱을 이용한 최적화와 연관이 있다). 그럼 또 다른 방법은 없을까?

Reference. MIT-TinyML-lecture05-Quantization-2 in https://efficientml.ai

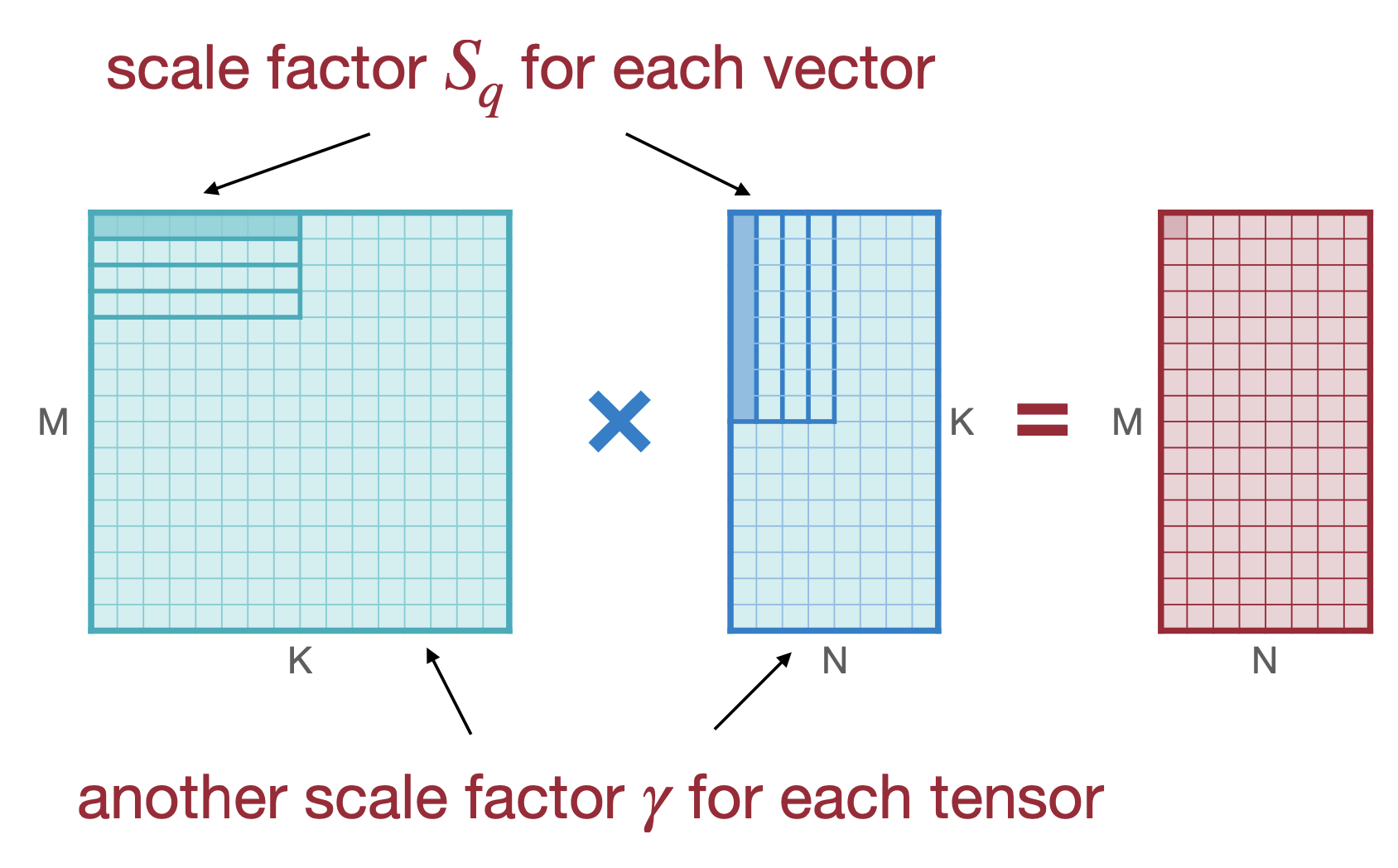
세 번째 방법은 Group Quantization으로 소개하는 Per-vector Scaled Quantization와 Shared Micro-exponent(MX) data type 이다. Per-vector Scaled Quantization은 2023년도 강의부터 소개하는데, 이 방법은 Scale factor를 그룹별로 하나, Per-Tensor로 하나로 두개를 두는 방법이다. 아래의 그림을 보면,

Reference. MIT-TinyML-lecture05-Quantization-2 in https://efficientml.ai

\[r=S(q-Z) \rightarrow r=\gamma \cdot S_{q}(q-Z)\]

\(S_q\) 로 vector별 스케일링을 하나, \(\gamma\) 로 Tensor에 스케일링을 하며 감마는 floating point로 하는 것을 볼 수있다. 아무래도 vector단위로 스케일링을 하게되면 channel과 비교해서 하드웨어 플랫폼에 맞게 accuracy의 trade-off를 조절하기 더 수월할 것으로 보인다.

여기서 강의는 지표인 Memory Overhead로 “Effective Bit Width”를 소개한다. 이는 Microsoft에서 제공하는 Quantization Approach MX4, MX6, MX9과 연결돼 있는데, 이 데이터타입은 조금 이후에 더 자세히 설명할 것이다. Effective Bit Width? 예시 하나를 들어 이해해보자. 만약 4-bit Quatization을 4-bit per-vector scale을 16 elements(4개의 weight가 각각 4bit를 가진다고 생각하면 16 element로 계산된다 유추할 있다) 라면, Effective Bit Width는 4(Scale bit) + 4(Vector Scale bit) / 16(Vector Size) = 4.25가 된다. Element당 Scale bit라고 간단하게 생각할 수도 있을 듯 싶다.

마지막 Per-vector Scaled Quantization을 이해하다보면 이전에 Per-Tensor, Per-Channel도 그룹으로 얼마만큼 묶는 차이가 있고, 이는 이들을 일반화할 수 있어 보인다. 강의에서 바로 다음에 소개하는 방법이 바로 Multi-level scaling scheme이다. Per-Channel Quantization와 Per-Vector Quantization(VSQ, Vector-Scale Quantization)부터 봐보자.

Reference. With Shared Microexponents, A Little Shifting Goes a Long Way [Bita Rouhani et al.]

Per-Channel Quantization는 Scale factor가 하나로 Effective Bit Width는 4가 된다. 그리고 VSQ는 이전에 계산했 듯 4.25가 될 것이다(참고로 Per Channel로 적용되는 Scale의 경우 element의 수가 많아서 그런지 따로 Effective Bit Width로 계산하지는 않는다). VSQ까지 보면서 Effective Bit Width는,

Effective Bit Width = Scale bit + Group 0 Scale bit / Group 0 Size +...
e.g. VSQ Data type int4 = Scale bit (4) + Group 0 Scale bit(4) / Group 0 Size(16) = 4.25

이렇게 계산할 수 있다. 그리고, MX4, MX6, MX9가 나온다. 참고로 S는 Sign bit, M은 Mantissa bit, E는 Exponent bit를 의미한다(Mantissa나 Exponent에 대한 자세한 내용은 floating point vs fixed point 글을 참고하자). 아래는 Microsoft에서 제공하는 Quantization Approach MX4, MX6, MX9에 대한 표이다.

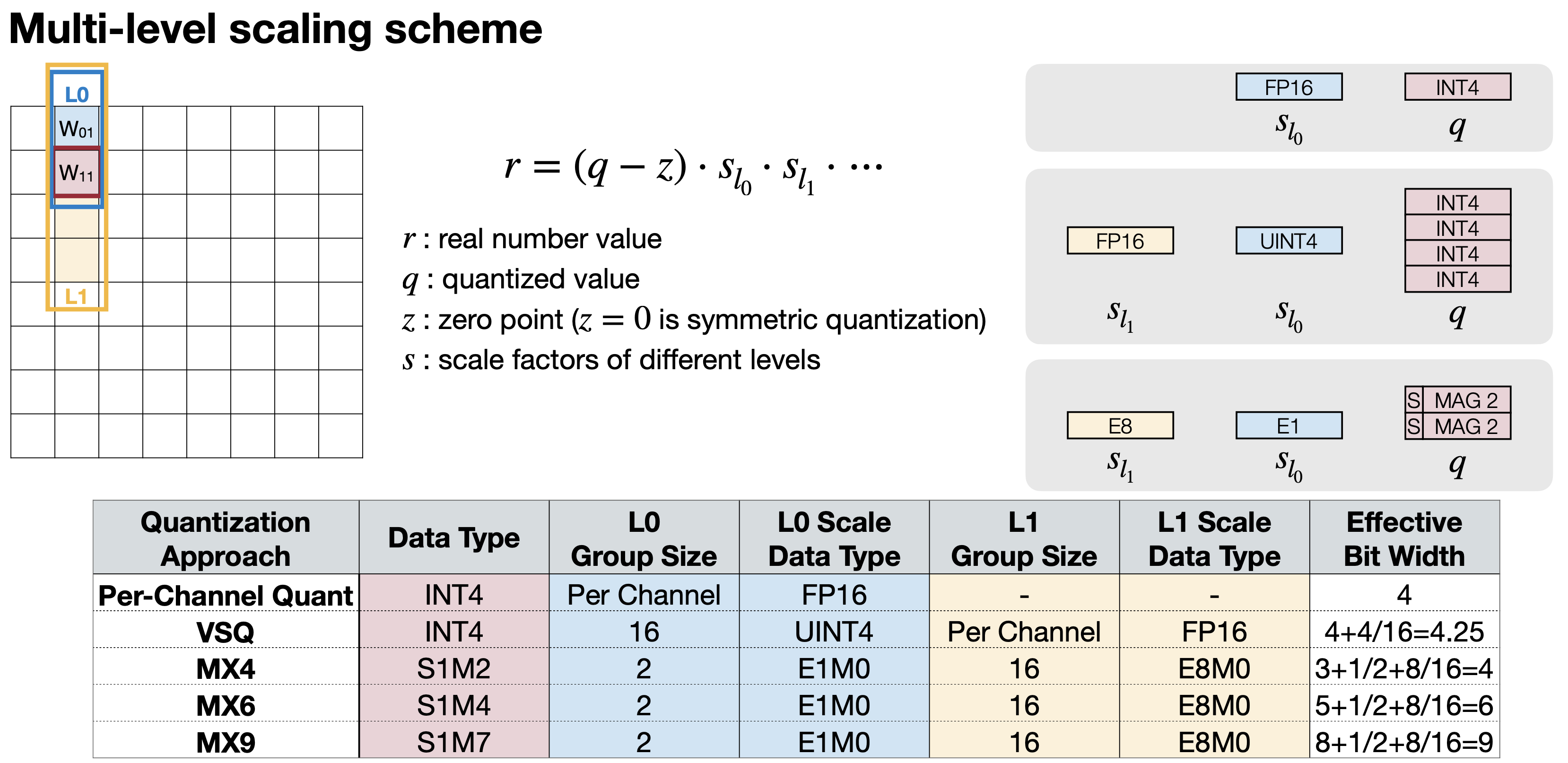
Reference. With Shared Microexponents, A Little Shifting Goes a Long Way [Bita Rouhani et al.]

2.1.2 Weight Equalization

여기까지 Weight Quatization에서 그룹으로 얼마만큼 묶는지에 따라(강의에서는 Granularity) Quatization을 하는 여러 방법을 소개했다. 다음으로 소개 할 방법은 Weight Equalization이다. 2022년에 소개해준 내용인데, 이는 i번째 layer의 output channel를 scaling down 하면서 i+1번째 layer의 input channel을 scaling up 해서 Scale로 인해 Quantization 전후로 생기는 Layer간 차이를 줄이는 방법이다.

Data-Free Quantization Through Weight Equalization and Bias Correction [Markus et al., ICCV 2019]

예를 들어 위에 그림처럼 Layer i의 output channel과 Layer i+1의 input channel이 있다. 여기서 식을 전개하면 아래와 같은데,

\[\begin{aligned} y^{(i+1)}&=f(W^{(i+1)}x^{(i+1)}+b^{(i+1)}) \\ &=f(W^{(i+1)} \cdot f(W^{(i)}x^{(i)}+b^{(i)}) +b^{(i+1)}) \\ &=f(W^{(i+1)}S \cdot f(S^{-1}(W^{(i)}x^{(i)}+S^{-1}b^{(i)})) +b^{(i+1)}) \end{aligned}\]

where \(S = diag(s)\) , \(s_j\) is the weight equalization scale factor of output channel \(j\)

여기서 Scale(S)가 i+1번째 layer의 weight에, i번째 weight에 1/S 로 Scale될 떄 기존에 Scale 하지 않은 식과 유사하게 유지할 있는 것을 볼 수 있다. 즉,

\[r^{(i)}_{oc_j} / s = r^{(i+1)}_{ic_j} \cdot s\\ s_j = \dfrac{1}{r^{(i+1)}_{ic=j}}\sqrt{r_{oc=j}^{(i)}\cdot r_{ic=j}^{(i+1)}} \\ r^{(i)}_{oc_j} = r^{(i)}_{oc_j} / s = \sqrt{r_{oc=j}^{(i)}\cdot r_{ic=j}^{(i+1)}} \\ r^{(i)}_{ic_j} =r^{(i)}_{ic_j} \cdot s = \sqrt{r_{oc=j}^{(i)}\cdot r_{ic=j}^{(i+1)}} \\\]

이렇게 하면 i번째 layer의 output channel과 i+1번째 layer의 input channel의 Scale을 각각 \(S\) 와 \(1/S\) 로하며 weight간의 격차를 줄일 수 있다.

2.1.3 Adaptive rounding

Reference. MIT-TinyML-lecture06-Quantization-2 in https://efficientml.ai

마지막 소개하는 방법은 Adaptive rounding 이다. 반올림은 Round-to-nearest으로 불리는 일반적인 반올림을 생각할 수 있고, 하나의 기준을 가지고 반올림을 하는 Adaptive Round를 생각할 할 수 있다. 강의에서는 Round-to-nearest가 최적의 방법이 되지 않는다고 말하며, Adaptive round로 weight에 0부터 1 사이의 값을 더해 수식처럼 \(\tilde{w} = \lfloor\lfloor w\rfloor + \delta\rceil, \delta \in [0, 1]\) 최적의 Optimal한 반올림 값을 구한다.

\[\begin{aligned} &argmin_V\lvert\lvert Wx-\tilde Wx\lvert\lvert ^2_F + \lambda f_{reg}(V) \\ \rightarrow & argmin_V\lvert\lvert Wx-\lfloor\lfloor W \rfloor + h(V) \rceil x\lvert\lvert ^2_F + \lambda f_{reg}(V) \end{aligned}\]

2.2 Activation quantization

두 번째로 Activation quantization이 있다. 모델결과로 나오는 결과를 직접적으로 결정하는 Activation Quatization에서는 두 가지를 고려한 방법을 소개한다. 하나는 Activation 레이어에서 결과값을 Smoothing한 분포를 가지게 하기 위해 Exponential Moving Average(EMA)를 사용하는 방법이고, 다른 하나는 다양한 입력값을 고려해 batch samples을 FP32 모델과 calibration하는 방법이다.

Exponential Moving Average (EMA)은 아래 식에서 \(\alpha\) 를 구하는 방법이다.

\[\hat r^{(t)}_{max, min} = \alpha r^{(t)}_{max, min} + (1-\alpha) \hat r^{(t)}_{max, min}\]

Calibration의 컨셉은 많은 input의 min/max 평균을 이용하자는 것이다. 그래서 trained FP32 model과 sample batch를 가지고 quantized한 모델의 결과와 calibration을 돌리면서 그 차이를 최소화 시키는데, 여기에 이용하는 지표는 loss of information와 Newton-Raphson method를 사용한 Mean Square Error(MSE)가 있다.

\[MSE = \underset{\lvert r \lvert_{max}}{min}\ \mathbb{E}[(X-Q(X))^2]\] \[KL\ divergence=D_{KL}(P\lvert\lvert Q) = \sum_i^N P(x_i)log\dfrac{P(x_i)}{Q(x_i)}\]

2.3 Quanization Bias Correction

마지막으로 Quatization으로 biased error를 잡는다는 것을 소개한다. \(\epsilon = Q(W)-W\) 이라고 두고 아래처럼 식이 전개시키면 마지막 항에서 보이는 \(-\epsilon\mathbb{E}[x]\) 부분이 bias를 quatization을 할 때 제거 된다고 한다(이 부분은 2023년에는 소개하진 않는데, 당연한 것이어서 안하는지, 혹은 영향이 크지 않아서 그런지는 모르겠다. Bias Quatization이후에 MobileNetV2에서 한 레이어의 output을 보면 어느정도 제거되는 것처럼 보인다).

\[\begin{aligned} \mathbb{E}[y] &= \mathbb{E}[Wx] + \mathbb{E}[\epsilon x] - \mathbb{E}[\epsilon x],\ \mathbb{E}[Q(W)x] = \mathbb{E}[Wx] + \mathbb{E}[\epsilon x] \\ \mathbb{E}[y] &= \mathbb{E}[Q(W)x] - \epsilon\mathbb{E}[x] \end{aligned}\]

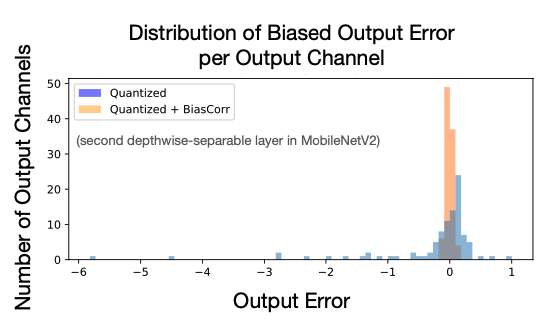
Reference. MIT-TinyML-lecture06-Quantization-2 in https://efficientml.ai

2.4 Post-Training INT8 Linear Quantization Result

앞선 Post-Training Quantization을 적용한 결과를 보여준다. 이미지계열 모델을 모두 사용했으며, 성능하락폭은 지표로 보여준다. 비교적 큰 모델들의 경우 준수한 성능을 보여주지만 MobileNetV1, V2와 같은 작은 모델은 생각보다 Quantization으로 떨어지는 성능폭(-11.8%, -2.1%) 이 큰 것을 볼 수 있다. 그럼 작은 크기의 모델들은 어떻게 Training 해야할까?

Reference. MIT-TinyML-lecture06-Quantization-2 in https://efficientml.ai

강의는 주로 MIT HAN LAB에서 진행된 연구를 중심으로 Quantization 방법을 설명한다. 내용이 길어, 다음 번 글에서 마저 작은 크기의 모델 훈련을 위한 Quantization 방법, 궁극의 Quatization인 Binary/Ternary Quantization, 그리고 Mixed Precision Quantization에 대해 이어서 이야기해보려 한다. 그리고, 이렇게 이론만 보면 아쉬우니 과제로 나온 Quantization 방법들을 코드로 구현해보는 것까지!

To be continued… (1/2)

*이어서 TinyML 스터디를 진행해 Quantization 1/2 편을 합친 포스트를 여기에 작성돼 있습니다.

Reference

PREVIOUSOptimization for tiny devices in C++ 2/2

NEXTPruning 1/2