DSP(Digital Signal Processing) 엔지니어로 일을 하게되면 “Fixed point”라는 개념을 많이 접하게 됩니다. 때문에 기존에 쓰던 덧셈, 뺄셈, 곱셈, 나눗셈, 제곱근과 같은 연산에 exponential이나 log는 연산량을 고려해 알고리즘을 짤 때, 골치아픈 경우가 많았습니다. 그런데 그냥 편하게 Floating point를 사용하면 되지, 왜 구지 Fixed point을 사용할까? Floating point로 프로그래밍에서 계산을 할 때 아래와 같은 결과는 어떻게 나올 수가 있는 걸까요? 이 질문에 답은 Floating point가 고안된 과정을 쭉 훑어보면 나올 수 있습니다.
\[0.1 + 0.1. = 0.20000000298023224 ?\]영상만드시는 분께 허락을 받아 youtube.com/watch?v=dQhj5RGtag0 영상에서 나오는 내용을 제 나름대로 정리한 것임을 미리 언급드립니다. 영어가 익숙하시다면 꼭 영상을 보시는 것을 추천드립니다.
1. Integer representation
컴퓨터에서 수를 표현하기 위해서 어떤 방법이 있을까요? 가장 쉽게 생각 할 수 있는 방법은 “이진수” 입니다.
| Binary bit | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|---|---|
| 2^7 | 2^6 | 2^5 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 | |
| Decimal | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
컴퓨터내에 있는 모든 숫자는 0과 1로 표현될 수 있는 것을 이용해 이진 수로 0과 양의 정수를 표현할 수 있죠. 위의 예시는 $100001001_{2} = 137$ 을 보여주고 있습니다. 그렇다면 32bit, 즉 int 혹은 int32로 선언한 변수의 메모리로 우리는 $2^{32}$의 수 까지 표현할 수 있는 것이죠.
2. Decimal representation
여기까지는 이해하는 데 그렇게 어렵지 않죠. 그럼 당연히 정수만 우리는 표현하진 않죠, 소수와 음수는 어떻게 표현할 수 있을까요? 먼저 소수를 살펴봅시다.
0000000000000001.1000000000000000
= 2^0+2^{-1} = 1.5
1111000010011111.1001001010101001
= DEC 61599.5727912354
생각 할 수 있는 간단한 소수를 표현하는 방법은 정수를 표현하기 위한 영역과 소수를 표현하기 위한 영역으로 나누는 겁니다. 위의 첫번째 예시처럼 $2^0+2^{-1}$로 수를 표현하면 우리는 $1.5$를 표현할 수 있죠. 이 방법을 우리는 Fixed point라고 부릅니다. 고정된 점을 이용한다… 이런 의미인 것 같죠?
3. Point index and Digits
그럼 fixed point 표기로 우리는 31개의 소수점자리를 표현할 수 있습니다. 그러면 그 소수점자리를 가리키는 “Point index” 와 실제 숫자인 “Mantissa”로 32bit을 채워 숫자를 표기할 수 있을 겁니다.
Point index(5bit) | Digits(Mantissa)(27bit)
11001 | 11.1100001001111110010010101
25 | 3.759739548
4. How to represent negative number?
그러면 음수는 어떻게 표현할 수 있을까요? 가장 간단한 방법은 Sign bit라고 맨 앞에 1비트가 0이면 양의 수, 1이면 음의 수로 표현하는 겁니다. 이외에도 2’s complement 방식도 있습니다.
5. Redundancy Problem
하지만 위와 같이 소수를 점으로 표현하게 되면 한 가지 문제가 생길 수 밖에 없습니다. 아래와 같이 그건 바로 수를 표현하는 데 공간을 낭비하고, 표현할 수 있는 수도 제한적이며, 이는 같은 메모리 공간에 같은 수를 표현하는 데 여러 표기가 있다는 것이 핵심 문제라는 것이죠.
Redundancy
001.10000000000000000000000000000
0000000000000000000001.10000000000
= DEC 1.5
그래서 이를 해결하는 방법이 바로 과학시간에 많이 배우는 Scientific Notation $4.937 \times 10^9$ 입니다.
6. Scientific Notation
\[4.937 \times 10^9\]왜 이 표기를 쓰기 시작한 걸까요? 영상에서는 한 숫자를 표현할 수 있는 “유일한 하나의 표현 방법”이 그 이유라고 설명합니다. 여기서 부터 아래의 예시처럼 mantissa는 항상 소수자리를 표현하게 됩니다.
sign | exponent | mantissa
1 01100010 1.0011100101100110100011
이렇게 된 숫자표기로 표현할 수 있는 범위는 영상 7:50에서 확인해주세요!
그리고 Scientific Notation에서 표기하는 방법을 보면 Mantissa의 첫 번째 bit는 항상 1인 것도 볼 수 있으실 겁니다(10진수는 1-9까지 있지만 2진수에서는 딱 1, 즉 한 bit만 사용하는 것인 거죠!). 여기서 이 항상 1인 digit을 leading bit이라고 부를 겁니다. 이 표현 방법이 바로 “Floating point” 입니다.
sign | exponent | mantissa
1 01100010 |1(always)|.|0011100101100110100011
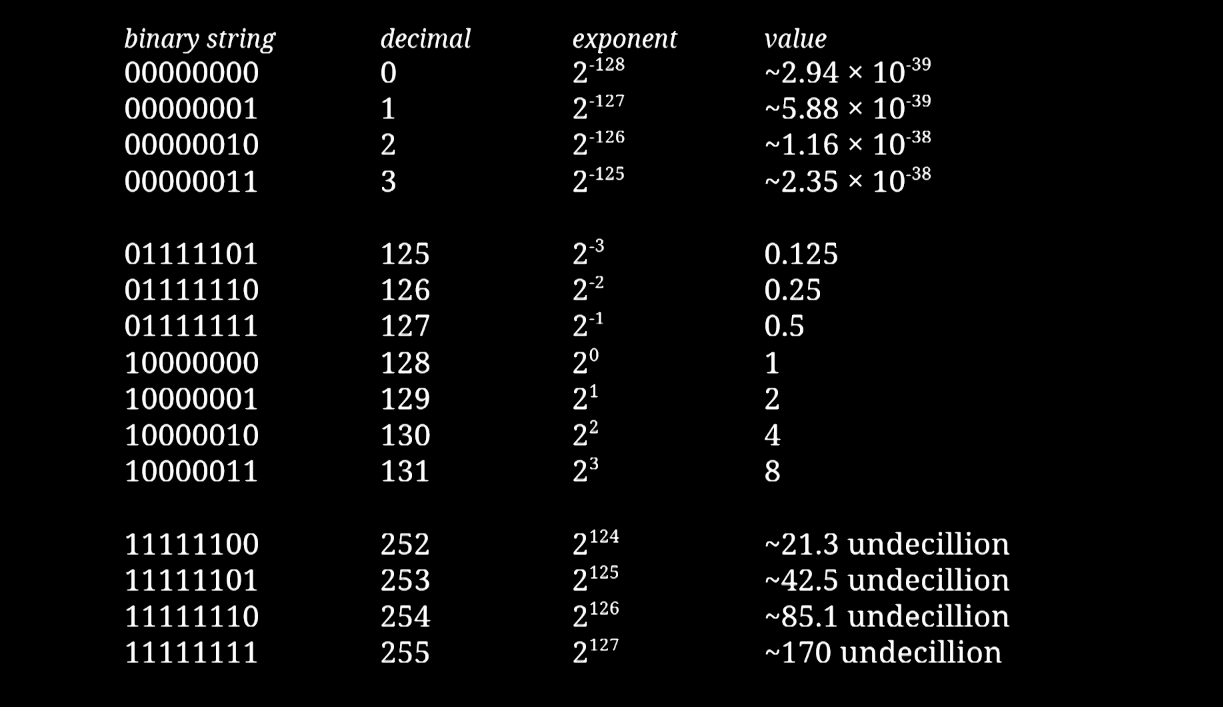
Reference. jan Misali's how floating point works
7. How to represent zero?
근데, 위와 표기하게 되면 문제가 한 가지 있습니다. 영상에서 숫자 범위를 보시면 알겠지만, 0을 표현할 수가 없게 됩니다. 그리고 다른 한 가지 문제는 exponent로 표현을 할 때 숫자 범위에 불균형을 보실 수 있습니다.
그렇게 0을 표기하기 가장 쉬운 방법은? 아래와 같이 모든 exponent의 bit가 0일 때 0이라고 할 수도 있겠죠.
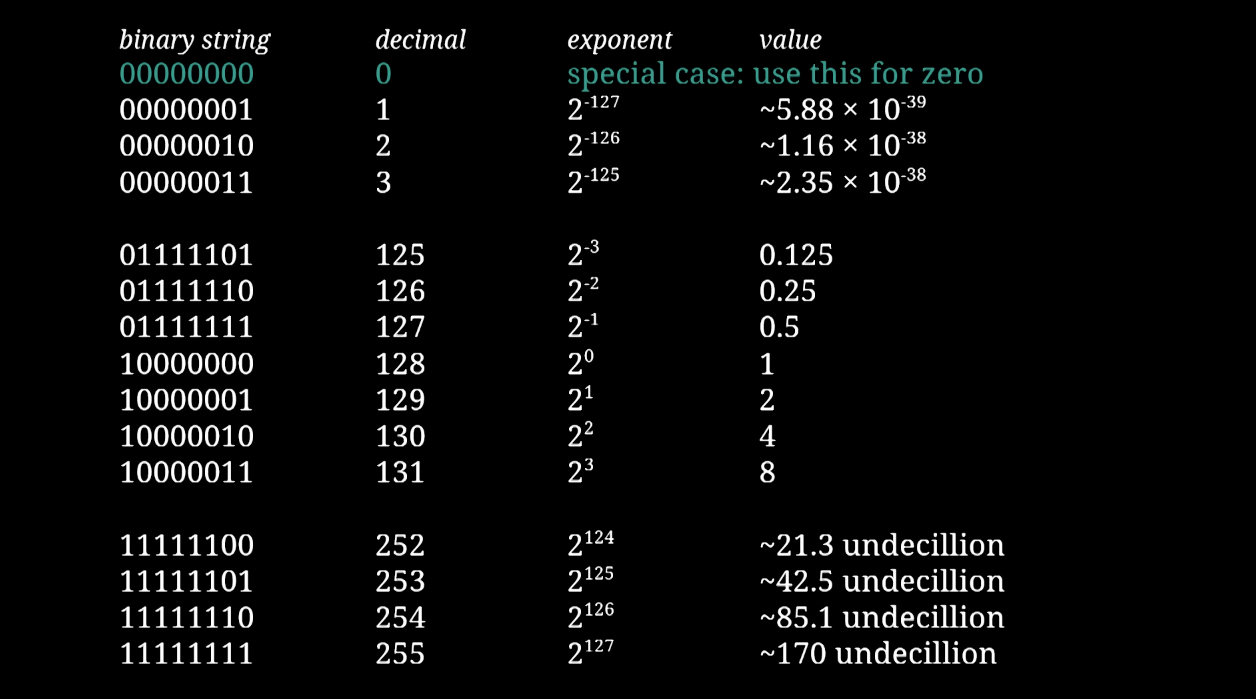
Reference. jan Misali's how floating point works
하지만 그러면 0이라고 표현할 수 있는 숫자가 너무 많아 질 겁니다. mantissa가 모두 0일 때 0이라고 정의해도 되겠지만, 영상에서는 “but it would be nice to put those bits to use so we’re not wasting all these potential number.”라고 이야기 합니다. 아마 비트를 모두 다 활용하는 방법을 사람들이 생각했던 것이겠죠?
이 문제를 해결하는 방법은 전혀 다른 문제를 해결하는 데서 발견하게 됩니다. 그 다른 문제는 “만약 이 시스템에서 가장 작은 두 수를 뺀다면 어떻게 표현해야할까?” 에서 나옵니다. 예를 들어 아래와 같은 상황이 있다고 생각해봅시다.
1.00011 x 2^{-127}
- 1.00011 x 2^{-127}
----------------------
= 0.00010 x 2^{-127} = 1.0 x 2^{-131}
이 수를 지금 표기방법으로는 0으로 할 수 밖에 없었습니다. 다른 방법은 없을까요? 여기서 중요한 한 가지 포인트가 잡습니다.
zero means that “zero” can actually have all sorts of values.
바로 “subnormal numbers” 입니다. 이 숫자는 “numbers that are too small to be represented normally” 로 만약에 exponent가 가장 작은 값이 되면 leading bit를 0으로 바꿔 버리는 거죠. 아래와 같이요.
sign | exponent | mantissa
1 00000000 0.0011100101100110100011
그러면 우리는 엄청 작은 수를 표현할 수 있는 숫자 표기법을 가질 수 있게 된 겁니다!
8. Philosophy of floating point, Estimation
“Floating point arithmetic is all about this compromise between precision and being able to use a wide range of numbers.”
이제 우리는 Floating point를 이용하면 $10^{15}$와 같이 어마어마하게 큰 수도 표현할 수 있죠. 하지만, 이 floating point number는 정확하게 그 숫자를 표기하지는 않습니다. “숫자의 범위” 를 표현하죠. 예를 들어서, 3의 경우에도 3이 아닌 3에 가장 가까운 floating point number를 표기합니다. 그럼 표현할 수 있는 범위가 어마어마하게 많겠죠? 그럼에도 mantissa의 bit수를 고려하면 그 범위는 매우 좁을 수 밖에 없을 겁니다. 실제로 3을 표현하는 floating point number다음의 숫자는 $1.10000000000000000000001_2 \times 2^1= 3.0000002384185791015625$ 입니다. 이정도 정밀도면 대부분 계산하는데는 크게 지장은 없을 겁니다. 만약 더 작은 정밀도를 원한다면, 64bit로 늘리면 되겠죠.
아직 숫자 표기에 $-0$이 있습니다. 사실 크게 문제가 될 것 같지 않지만, 위의 수를 표현하고자 하는 철학(?)으로 이 문제 또한 해결하고자 한 표기법이 바로 “IEEE single-precision floating point standard”입니다.
9. How to represent Big number?

Reference. jan Misali's how floating point works
매우 큰 수는 어떨까요? 작은 수와 마찬가지로 exponent가 모두 1인 경우를 가장 큰 수 Infinity라고 두게 된다면, 작은 수떄와 동일하게 mantissa의 숫자가 바뀌어도 똑같은 Infinity를 가리키게 됩니다.
sign | exponent | mantissa
1 11111111 1.0000000000000000000000
- Infinity
sign | exponent | mantissa
1 11111111 1.0000000000000010000000
Not a Number(NaN)
우리는 exponent가 모두 1이며 동시에 mantissa가 모두 0인 경우에 Infinitiy라고 부를 겁니다. 그리고 그 상태에서 mantissa가 모두 0이 아닌 경우를 Not a Number(NaN)이라고 부를 거죠.
10. Calculation between zero and infinity
이렇듯, floating number와 실제 숫자에서 가장 큰 차이는 0이 표현하는 바입니다.
그럼 0과 $\infty$ 에서 몇 가지 조합이 생길 수 있겠네요.
\[\begin{aligned} 1/0 &= \infty\\ -1/0 &= \infty \\ 0/0 &= \text{NaN}\\ 0 \times \infty &= \text{NaN} \end{aligned}\]네, 바로 0/0 을 정의하기 위해서 Not a Number(NaN)를 정의합니다. $0 \times \infty$의 경우도 [a number that’s too small to store] x [a number that’s too large to store] 인데, 수의 범위를 정할 수 없으니 이 경우도 Not a Number(NaN)가 되는 거죠. NaN은 즉, “Invalid operation”을 위해서 태어난 친구인 것이죠.
11. Epilogue
참고로 Wiki에서 볼 수 있는 IEEE 754 정의하고 있는 32bit Floating point number의 예시는 다음과 같습니다.

Reference. wikipedia-Floating-point-arithemetic
위에서 주의할 점은 leading bit는 이미 fraction에서 빠져 있다는 점이다. 따라서 위를 식으로 쓰자면,
\[\text{exp} = 0*2^{7} + 1*2^{6} + 1*2^{5} + 1*2^{4} + 1*2^{3} + 1*2^{2} + 0*2^{1} + 0*2^{0} - 127\\ frac = 1 + 0*2^{-1} + 1*2^{-1} + 0*2^{-1}... + 0*2^{-23} \\ \text{decimal number} = \text{exp} * \text{frac} = 0.15625\]여기까지 이해하고 난 다음 든 질문은 “그러면 왜 DSP에서는 Fixed point를 사용하고 있는 거지? 였습니다. Floating point number를 보게되면 부가적인 숫자기호들을 볼 수 있을 겁니다. 예를 들어 NaN, $\infty$ 와 같은 기호들이 있죠. 그 기호들은 어떻게 연산처리해야 할까요? 그 기호들을 추가로 넣는다면 연산량에 차이가 없을까요? 이 Floating point number를 계산하기 위한 하드웨어를 설명하는 영상을 보시면, Fixed point가 특정 분야에서는 쓰일 수 밖에 없다는 것이 어느정도 납득이 갑니다.
연산량이 정말 다를까에 대해서 조금 더 찾아보니, 이 글 에서는 아래와 같이 이야기 합니다.
The paper mentioned by njuffa, Cristina Iordache and Ping Tak Peter Tang, An Overview of Floating-Point Support and Math Library on the Intel XScale Architecture supports this. For the Intel XScale processor the list as latencies (excerpt):
integer addition or subtraction: 1 cycle
integer multiplication: 2-6 cycles
fp addition (emulated): 34 cycles
fp multiplication (emulated): 35 cycles
이와 관련해서는 추후에 테스트를 해보고 추가적으로 덧붙일 예정입니다.
여기까지 정수, 소수, 음수, 더 넓은 숫자를 위한 표기법, 가장 작은 수들, 가장 큰 수들, IEEE가 생각하는 숫자의 철학까지 현재 정의하고 있는 Floating number에 대한 IEEE 흐름을 살펴봤습니다. 이제 숫자를 배워봤으니, 다음 차례로 차근차근 신호처리를 들어가 보겠습니다.
Reference
- jan Misali’s how floating point works youtube.com/watch?v=dQhj5RGtag0
- NaN and Hardware floating point, and FLOP https://www.youtube.com/watch?v=5TFDG-y-EHs
- Fast Inverse Square Root: A Quake 3 Algorithm using floating point format https://www.youtube.com/watch?v=p8u_k2LIZyo
- IEEE 754: https://en.wikipedia.org/wiki/Floating-point_arithmetic