All contents is arranged from CS224N contents. Please see the details to the CS224N!
1. Intro
-
Create a model such that given the center word “jumped”, the model will be able to predict or generate the surrounding words “The”, “cat”, “over”, “the”, “puddle”.
→ Predicts the distribution (probability) of context words from a center word.
-
we essentially swap our x and y
i.e. x in the CBOW are now y and vice-versa.
- The input one-hot vector (center word) we will represent with an x (since there is only one).
- The output vectors as $y^{(j)}$.
- We define V and U the same as in CBOW.
2. Steps
-
Generate one hot input vector
$x \in \mathbb{R}^{\lvert V\lvert}$ of the center word
- We get our embedded word vector for the center word $v_c = \nu x \in \mathbb{R}^n$
- Generate a score vector z = $uv_c$
-
Turn the score vector into probabilities, $\hat{y} = softmax(z)$
- $\hat{y} _{c-m}, \ \dots, \ \hat{y} _{c-1},\ \hat{y} _{c+1},\ \dots,\ \hat{y} _{c+m}$ are the probabilities of observing each context word.
- We desire our probability vector generated to match the true prob- abilities which is $y^{(c−m)},\ \dots ,\ y^{(c−1)},\ y^{(c+1)},\ \dots ,\ y^{(c+m)}$, the one hot vectors of the actual output.
- Invoke a Naive Bayes assumption to break out the probabilities. If you have not seen this before, then simply put, it is a strong (naive) conditional independence assumption. In other words, given the center word, all output words are completely independent.
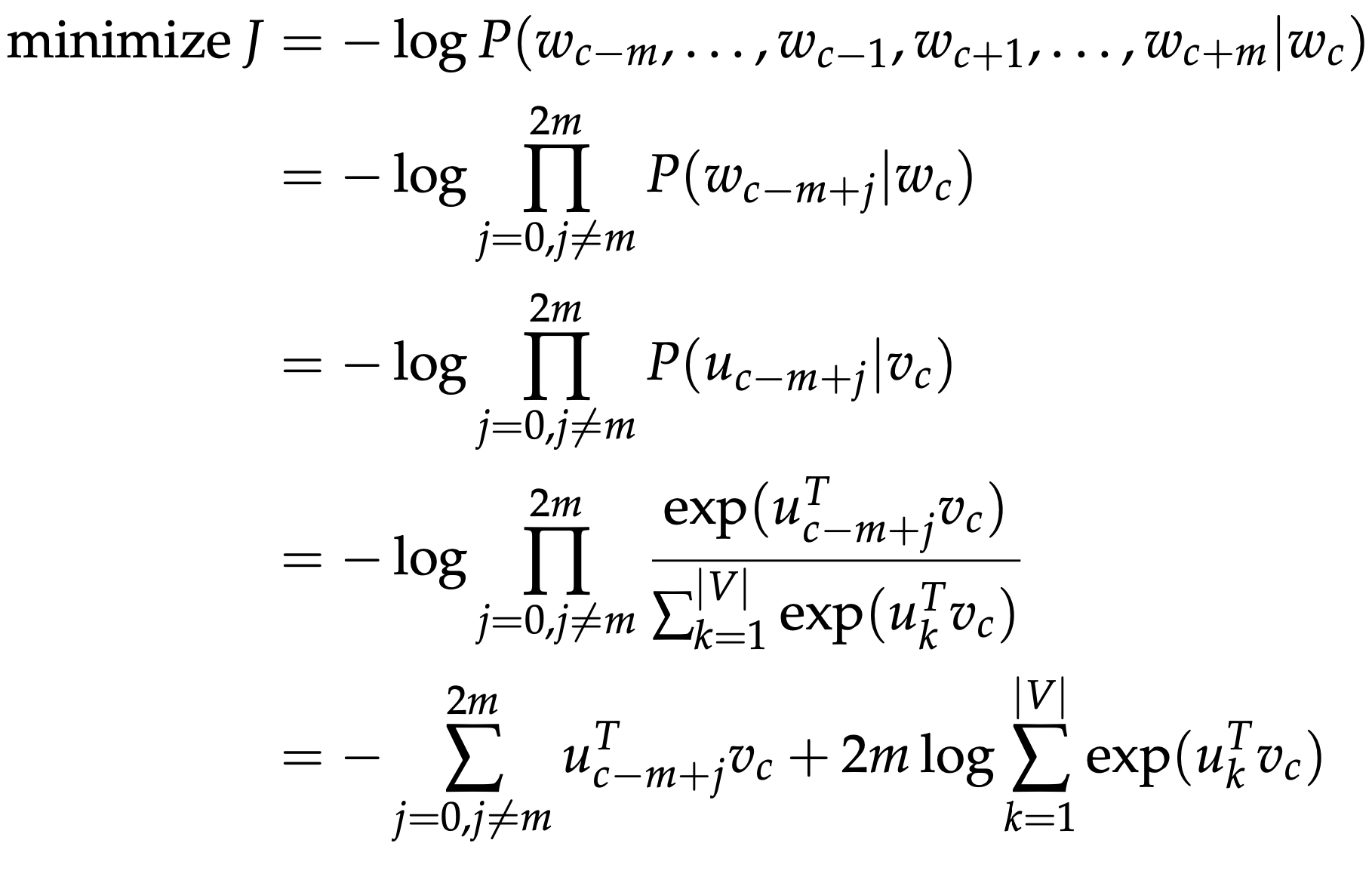
Reference. cs224n-2019-notes01-wordvecs1
- With this objective function, we can compute the gradients with respect to the unknown parameters and at each iteration update them via Stochastic Gradient Descent.
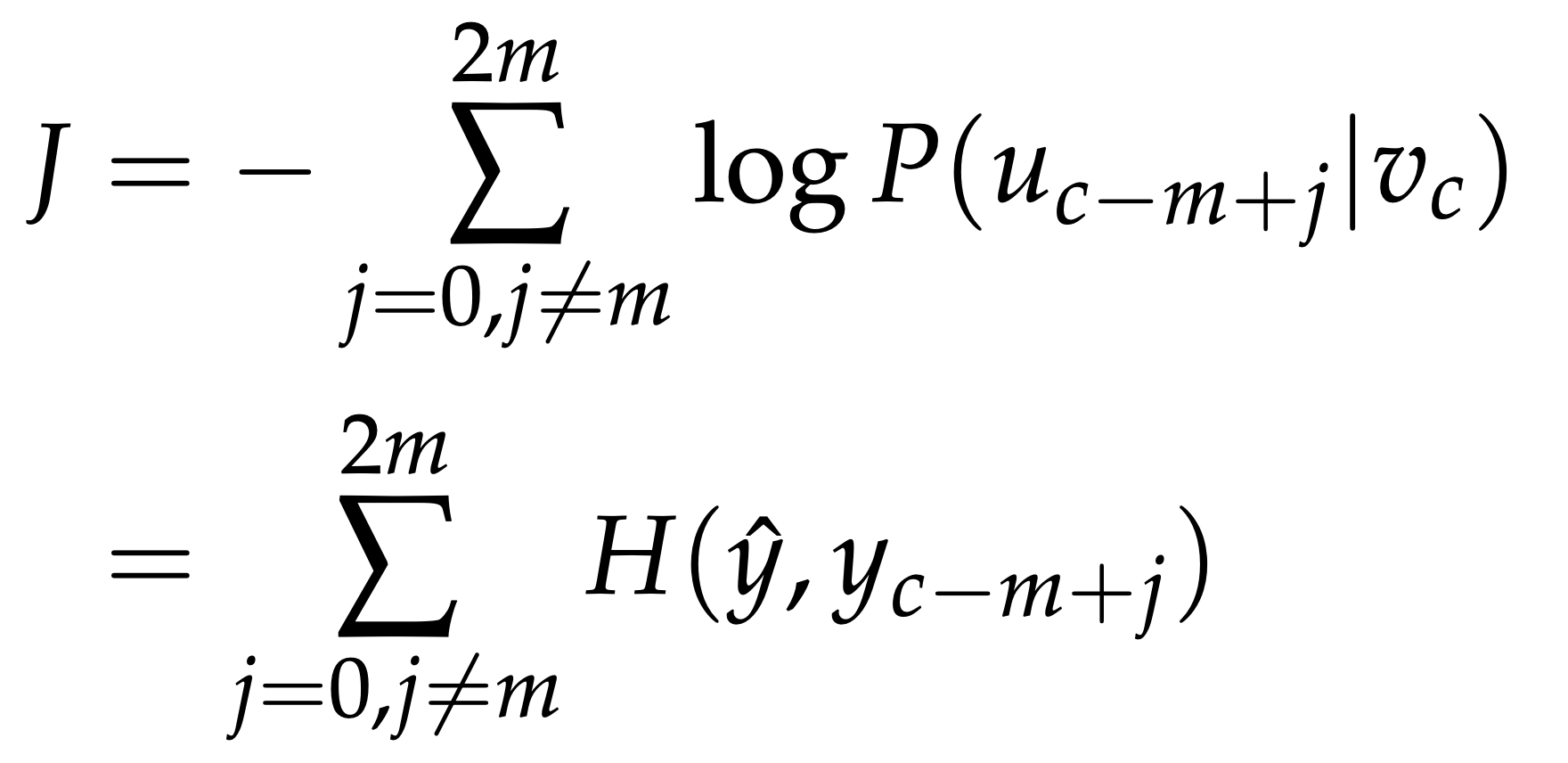
Reference. cs224n-2019-notes01-wordvecs1
H($\hat{y}, y_{c−m+j}$) is the cross-entropy between the probability vector $\hat{y}$ and the one-hot vector $y_{c−m+j}$