Negative Sampling

All contents is arranged from CS224N contents. Please see the details to the CS224N!

1. Intro

• It is inefficient to sample everything from the whole word dictionary.

  → Locally sampling only the periphery

• Problem: The summation over $\lvert V \lvert$ is computationally huge! Any update we do or evaluation of the objective function would take $O(\lvert V \lvert)$ time which if we recall is in the millions

• We “sample” from a noise distribution $P_n(w)$ whose probabilities match the ordering of the frequency of the vocabulary. To augment our formulation of the problem to incorporate Negative Sampling, all we need to do is update the:

  • objective function
  • gradients
  • update rules

2. Step

1. Denote by $P(D = 1 \lvert w, c)$ the probability that $(w, c)$ came from the corpus data. Correspondingly, $P(D = 0\lvert w, c)$ will be the probability that $(w, c)$ did not come from the corpus data.

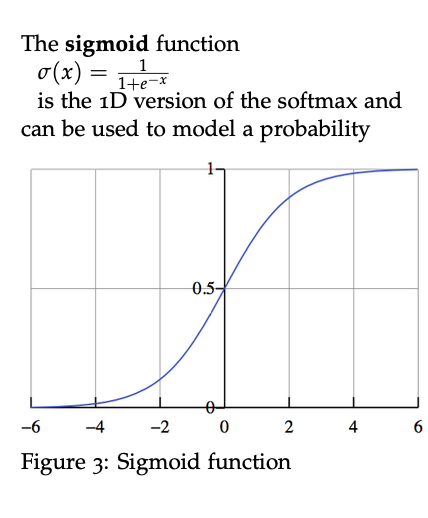
   First, let’s model $P(D = 1\lvert w, c)$ with the sigmoid function:

   \[P(D = 1 \lvert w,c,\theta) = \sigma(v_c^T v_w) = \dfrac{1}{1+e^{-v_c^T v_w}}\]

   • The sigmoid function

     

     Reference. cs224n-2019-notes01-wordvecs1

2. Build a new objective function that tries to maximize the probability of a word and context being in the corpus data if it indeed is, and maximize the probability of a word and context not being in the corpus data if it indeed is not.

   • We take a simple maximum likelihood approach of these two probabilities. (Here we take θ to be the parameters of the model, and in our case it is V and U.)
   \[\begin{aligned} \theta &= \underset{\theta}{argmax} \displaystyle\prod_{(w,c)\in D} P(D=1\lvert w,c,\theta) \displaystyle\prod_{(w,c)\in \tilde{D}} P(D=0\lvert w,c,\theta) \\ &= \underset{\theta}{argmax} \displaystyle\prod_{(w,c)\in D} P(D=1\lvert w,c,\theta) \displaystyle\prod_{(w,c)\in \tilde{D}} (1 - P(D=1\lvert w,c,\theta)) \\ &= \underset{\theta}{argmax} \displaystyle\sum_{(w,c)\in D} log P(D=1\lvert w,c,\theta) + \displaystyle\sum_{(w,c)\in \tilde{D}} log (1 - P(D=1\lvert w,c,\theta)) \\ &= \underset{\theta}{argmax} \displaystyle\sum_{(w,c)\in D} log \dfrac{1}{1+exp(-u_w^Tv_c)} + \displaystyle\sum_{(w,c)\in \tilde{D}} log (1 - \dfrac{1}{1+exp(-u_w^Tv_c)}) \\ &= \underset{\theta}{argmax} \displaystyle\sum_{(w,c)\in D} log \dfrac{1}{1+exp(-u_w^Tv_c)} + \displaystyle\sum_{(w,c)\in \tilde{D}} log (\dfrac{1}{1+exp(u_w^Tv_c)}) \\ \end{aligned}\]
   • Maximizing the likelihood is the same as minimizing the negative log-likelihood
   \[J = - \displaystyle\sum_{(w,c)\in D} log \dfrac{1}{1+exp(-u_w^Tv_c)} - \displaystyle\sum_{(w,c)\in \tilde{D}} log (\dfrac{1}{1+exp(u_w^Tv_c)})\]

• $\tilde{D}$ is a “false” or “negative” corpus.

3. Where we would have sentences like “stock boil fish is toy”

• Unnatural sentences that should get a low probability of ever occurring.
• We can generate $\tilde{D}$ on the fly by randomly sampling this negative from the word bank.

4. New objective function

• For Skip-Gram

  

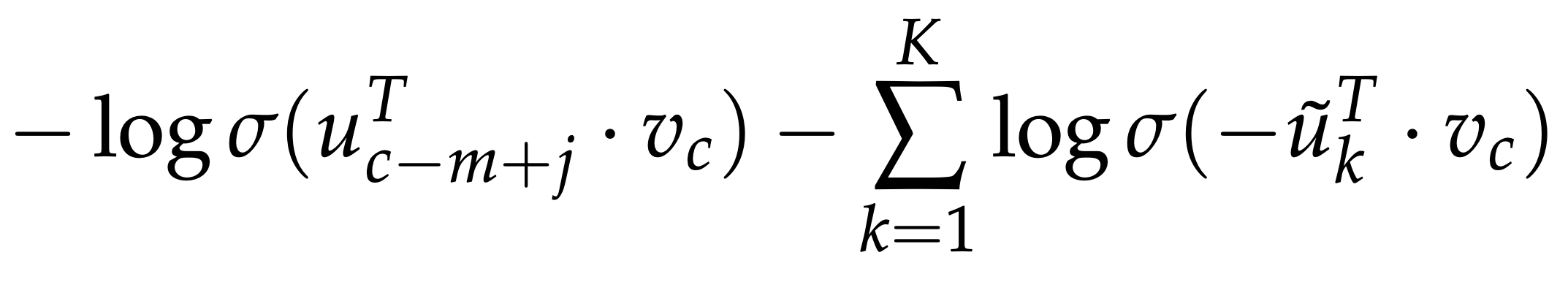
  Reference. cs224n-2019-notes01-wordvecs1

• For CBOW $\hat v = \dfrac{v_{c−m}+v_{c−m+1}+…+v_{c+m}}{2m}$

  

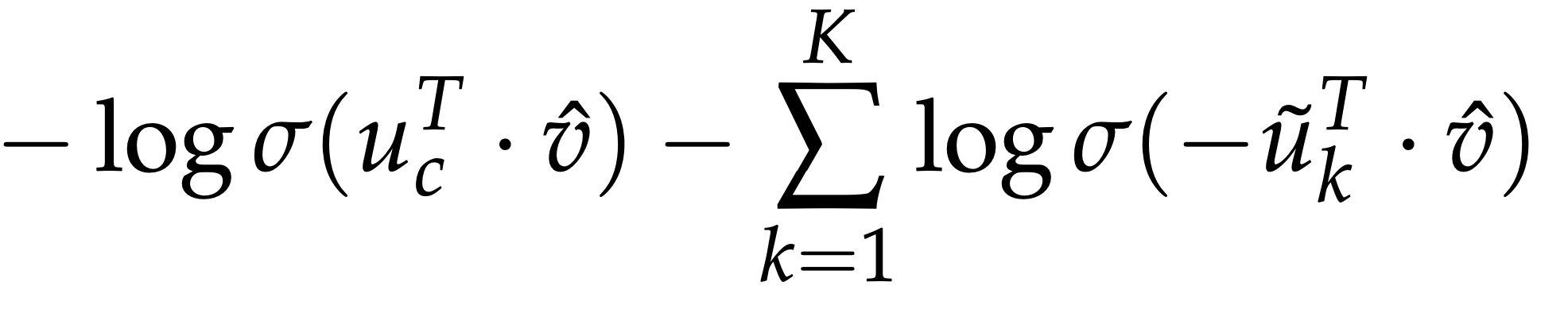
  Reference. cs224n-2019-notes01-wordvecs1

5. Why power is more proper to apply sampling?

In the above formulation, { $\text{~u}_k \lvert k = 1 \dots K $ } are sampled from $P_n(w)$. Let’s discuss what $Pn(w)$ should be. While there is much discussion of what makes the best approximation, what seems to work best is the Unigram Model was raised to the power of 3/4. Why 3/4?

Here’s an example that might help gain some intuition:

is: $0.9^{3/4}$ = 0.92

Constitution: $0.09^{3/4}$ = 0.16

bombastic: $0.01^{3/4}$ = 0.032

“Bombastic” is now 3x more likely to be sampled while “is” only went up marginally.

6. Reference

• Reference. Mikolov et al., 2013
• Korean Reference: https://wikidocs.net/22660
• Block Diagram: https://myndbook.com/view/4900
• Detail: [Rong, 2014] Rong, X. (2014). word2vec parameter learning explained. CoRR, abs/1411.2738.
• Hierarchical Softmax: [Mikolov et al., 2013] Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013). Efficient estimation of word representations in vector space. CoRR, abs/1301.3781.